The first step in this direction is to define cosets. For any subgroup \({H\subset G}\) and element \({g\in G}\), the set \({gH\equiv\left\{ gh\mid h\in H\right\} }\) is called a left coset of \({H}\) in \({G}\). Right cosets are defined similarly, and \({g}\) is called a representative element of the coset \({gH}\). Cosets can be viewed as a partitioning of all of \({G}\) into equal-sized disjoint “copies.” However, this cannot be used to define a group quotient \({G/H}\) since in general, the cosets themselves do not form a group.

A normal subgroup (AKA invariant subgroup, self-conjugate subgroup) of \({G}\), denoted \({N\triangleleft G}\), is defined as follows:

\(\displaystyle N\triangleleft G\:\textrm{if}\: gN=Ng\:\forall g\in G\Leftrightarrow gNg^{-1}\subseteq N\:\forall g\in G \)

Note that an immediate consequence of the above definition is that any subgroup of an abelian group is normal. It is not hard to see that the cosets of \({N}\) in \({G}\) (left and right being identical) do in fact comprise the elements of a group under the group operation \({(gN)(hN)\equiv\left\{ gnhm\mid n,m\in N\right\} =(gh)N}\). We denote this group \({G/N}\) and call it a quotient group (AKA factor group).

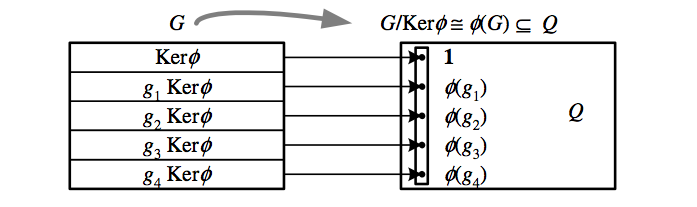
The kernel of a homomorphism \({\phi}\) from \({G}\) to another group \({Q}\) is the subgroup of elements that are mapped to the identity \({\mathbf{1}}\). Any normal subgroup \({N}\) is then the kernel of the group homomorphism \({\phi\colon G\to G/N}\) defined by \({g\mapsto gN}\), and thus all normal subgroups are homomorphism kernels. The converse of this is also true: for any homomorphism \({\phi\colon G\to Q}\), \({\textrm{Ker}\phi}\) is normal in \({G}\). Furthermore, the quotient group is isomorphic to the subgroup \({\phi\left(G\right)}\) of \({Q}\), so that we have the equation \({G/\textrm{Ker}\phi\cong\phi\left(G\right)}\), called the first isomorphism theorem or the fundamental theorem on homomorphisms: \({\phi}\) shrinks each equal-sized coset of \({G}\) to an element of \({\phi\left(G\right)}\), which is therefore a kind of simpler approximation to \({G}\).

It is helpful to demonstrate quotient groups with an easy example. Let \({\phi\colon\mathbb{Z}\to\mathbb{Z}_{3}}\) be the (surjective) homomorphism that sends each element to its remainder after being divided by 3. The kernel of this homomorphism is the subgroup of \({\mathbb{Z}}\) consisting of all integers of the form \({3n}\). Then the cosets \({\mathbb{Z}/\left\{ 3n\right\} }\) are the subgroups \({\left\{ 3n\right\} }\), \({\left\{ 3n+1\right\} }\), and \({\left\{ 3n+2\right\} }\), which are isomorphic to the elements of \({\mathbb{Z}_{3}}\).