If we take the exterior covariant derivative of the torsion, we get
\(\displaystyle \mathrm{D}\vec{T}=\mathrm{DD}\vec{\beta}=\check{R}\wedge\vec{\beta}. \)
This is called the first (AKA algebraic) Bianchi identity. Using the antisymmetry of \({\check{R}}\), we can write the first Bianchi identity explicitly as
\(\displaystyle \mathrm{D}\vec{T}(u,v,w)=\check{R}(u,v)\vec{w}+\check{R}(v,w)\vec{u}+\check{R}(w,u)\vec{v}, \)
which after working into index notation may be written
\(\displaystyle R^{a}{}_{[bcd]}=\nabla_{[b}T^{a}{}_{cd]}-T^{f}{}_{[bc}T^{a}{}_{d]f}. \)
In the case of zero torsion, this identity becomes \({\check{R}\wedge\vec{\beta}=0}\), which in index notation can be written \({R^{a}{}_{[bcd]}=0}\).
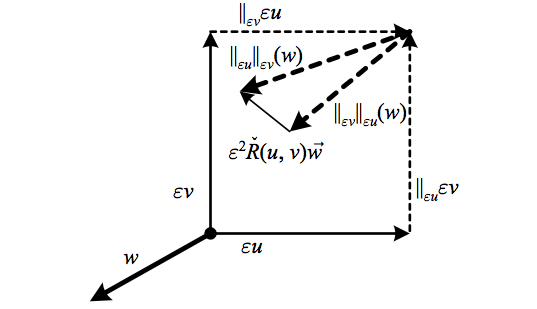
We can find a geometric interpretation for this identity by first constructing a variant of our picture of \({\check{R}(u,v)\vec{w}}\) as the change in \({\vec{w}}\) after being parallel transported in opposite directions around a loop. Taking advantage of our previous result that \({\check{R}(u,v)\vec{w}}\) only depends upon the local values of \({u}\) and \({v}\), we are free to construct their vector field values such that \({[u,v]=0}\). We then examine the difference between \({\vec{w}}\) being parallel transported in each direction halfway around the loop. For infinitesimal parallel transport from a point \({p}\) along a curve \({C}\) with tangent \({v}\) we have \({\parallel_{\varepsilon v}(w\left|_{p}\right.)\equiv\parallel_{C}(w\left|_{p}\right.)=w\left|_{p+\varepsilon v}\right.-\varepsilon\nabla_{v}w\left|_{p}\right.}\). Therefore we find that
\begin{aligned}\parallel_{\varepsilon u}\parallel_{\varepsilon v}(w\left|_{p}\right.) & =\parallel_{\varepsilon u}\left(w\left|_{p+\varepsilon v}\right.-\varepsilon\nabla_{v}w\left|_{p}\right.\right)\\ & =w\left|_{p+\varepsilon v+\varepsilon u}\right.-\varepsilon\nabla_{v}w\left|_{p+\varepsilon u}-\varepsilon\nabla_{u}w\left|_{p+\varepsilon v}\right.+\varepsilon^{2}\nabla_{u}\nabla_{v}w\left|_{p},\right.\right. \end{aligned}
so that
\begin{aligned}\parallel_{\varepsilon u}\parallel_{\varepsilon v}(w\left|_{p}\right.)-\parallel_{\varepsilon v}\parallel_{\varepsilon u}(w\left|_{p}\right.) & =\varepsilon^{2}\nabla_{u}\nabla_{v}w\left|_{p}\right.-\varepsilon^{2}\nabla_{v}\nabla_{u}w\left|_{p}\right.\\ & =\varepsilon^{2}\check{R}(u,v)\vec{w}, \end{aligned}
since \({[u,v]=0}\) means that \({w\left|_{p+\varepsilon v+\varepsilon u}\right.=w\left|_{p+\varepsilon u+\varepsilon v}\right.}\). In the case of zero torsion, we can further take advantage of our freedom in choosing the vector field values of \({u}\) and \({v}\) by requiring them to equal their parallel transports, i.e. \({v\left|_{p+\varepsilon u}\right.\equiv\parallel_{\varepsilon u}(v\left|_{p}\right.)}\) and \({u\left|_{p+\varepsilon v}\right.\equiv\parallel_{\varepsilon v}(u\left|_{p}\right.)}\), preserving the property \({[u,v]=0}\) due to the vanishing torsion.
The above depicts a slight variant of \({\check{R}\left(u,v\right)\vec{w}}\) viewed as “the difference between \({w}\) when parallel transported around the two opposite edges of the boundary of the surface defined by its arguments.” In the case of zero torsion, the boundary can be built from parallel transports instead of vector field values.
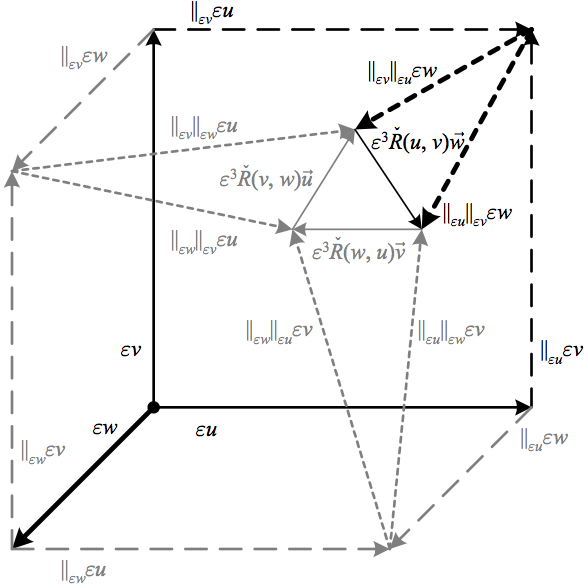
Thus, still assuming zero torsion, we can construct a cube from the parallel transports of \({u}\), \({v}\), and \({w}\). This construction reveals that the first Bianchi identity corresponds to the fact that the three curvature vectors form a triangle, i.e. their sum is zero.
The above depicts how the first Bianchi identity reflects the fact that for zero torsion, the far corners of a cube made of parallel transported vectors do not meet, and their separation is made up of the differences in parallel transport via opposite edges of each face. Note that the corners of the triangle are points since vanishing torsion means that e.g. \({\varepsilon u+\parallel_{\varepsilon u}(\varepsilon w)=\varepsilon w+\parallel_{\varepsilon w}(\varepsilon u)}\), so that the top point of the triangle reflects this equality parallel transported by \({\varepsilon v}\).