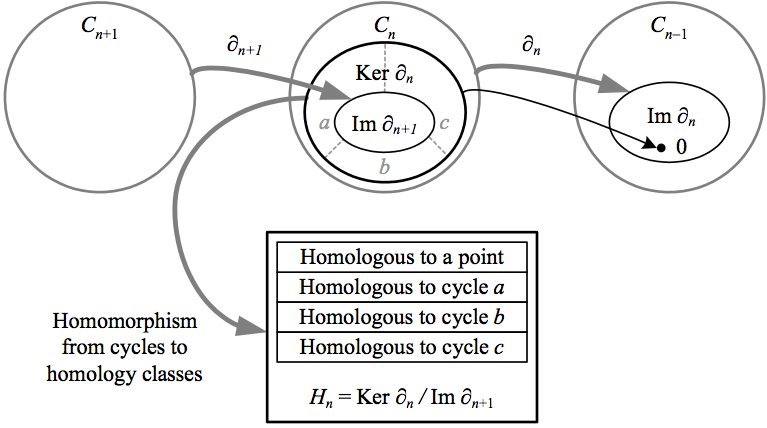
We can now define the homology groups (AKA singular homology groups). In the below definitions, \({\textrm{Ker}}\) denotes kernel and \({\textrm{Im}}\) denotes image.
- Cycle: an element of \({\textrm{Ker}\partial_{n}}\), i.e. an \({n}\)-surface in \({X}\) that has no boundary
- Boundary: an element of \({\textrm{Im}\partial_{n+1}}\), i.e. the boundary of an \({(n+1)}\)-volume in \({X}\)
- Homology class: an element of the homology group \({H_{n}(X)\equiv\textrm{Ker}\partial_{n}/\textrm{Im}\partial_{n+1}}\), i.e. a coset consisting of homologous \({n}\)-cycles that can all be obtained from each other by adding the boundary of some \({(n+1)}\)-volume in \({X}\)
| ◊ We can think of a typical cycle as a loop for \({n=1}\) or a sphere for \({n=2}\). Then the typical boundary is the chain of \({n}\)-cycles that form the edge of an arbitrary surface for \({n=1}\) or the surface of an arbitrary volume for \({n=2}.\) |
The cylinder and punctured plane in the figure on triangulations depict examples of homologous loops, two 1-chains that are the boundary of a 2-chain. The abelian group \({H_{n}(X)}\) is then generated by the cosets of non-homologous \({n}\)-cycles, thus counting the number of “\({n}\)-dimensional holes” in \({X}\).