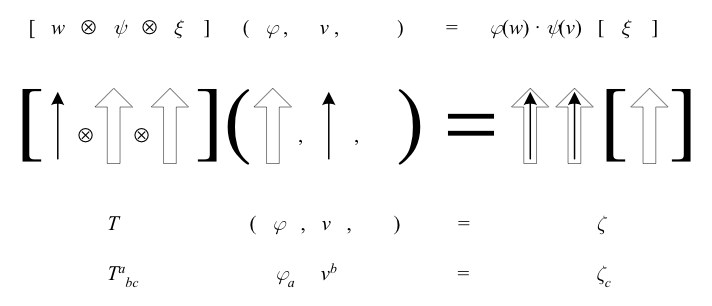There is an obvious multiplication of two 1-forms: the scalar multiplication of their values. The resulting object \({\varphi\psi\colon V\times V\to\mathbb{R}}\) is a nondegenerate bilinear form on \({V}\). Viewed as an “outer product” on \({V^{*}}\), multiplication is trivially seen to be a bilinear operation, i.e. \({a\left(\varphi+\psi\right)\xi=a\varphi\xi+a\psi\xi}\). Thus the product of two 1-forms is isomorphic to their tensor product.

We can extend this to any tensor by viewing vectors as linear mappings on 1-forms, and forming the isomorphism \({\bigotimes\varphi_{i}\mapsto\prod\varphi_{i}}\). Note that this isomorphism is not unique, since for example any real multiple of the product would yield a multilinear form as well. However it is canonical, since the choice does not impose any additional structure, and is also consistent with considering scalars as tensors of type \({\left(0,0\right)}\).

We can thus consider tensors to be multilinear mappings on \({V^{*}}\) and \({V}\). In fact, we can view a tensor of type \({\left(j,k\right)}\) as a mapping from \({l<j}\) 1-forms and \({m<k}\) vectors to the remaining \({\left(j-l\right)}\) vectors and \({\left(k-m\right)}\) 1-forms.

The above shows different ways of depicting a pure tensor of type \({\left(1,2\right)}\). The first line explicitly shows the tensor as a mapping from a 1-form \({\varphi}\) and a vector \({v}\) to a 1-form \({\xi}\). The second line visualizes vectors as arrows, and 1-forms as receptacles that when matched to an arrow yield a scalar. The third line combines the constituent vectors and 1-forms of the tensor into a single symbol \({T}\) while merging the scalars into \({\xi}\) to define \({\zeta}\), and the last line adds indices (covered in the next section).

A general tensor is a sum of pure tensors, so for example a tensor of the form \({\left(u\otimes\varphi\right)+\left(v\otimes\psi\right)}\) can be viewed as a linear mapping that takes \({\xi}\) and \({w}\) to the scalar \({\xi\left(u\right)\cdot\varphi\left(w\right)+\xi\left(v\right)\cdot\psi\left(w\right)}\). Since the roles of mappings and arguments can be reversed, we can simplify things further by viewing the arguments of a tensor as another tensor: \({\left(u\otimes\varphi\right)\left(\xi\otimes w\right)\equiv\left(u\otimes\varphi\right)\left(\xi,w\right)=\left(\xi\otimes w\right)\left(u,\varphi\right)=\xi\left(u\right)\cdot\varphi\left(w\right)}\).