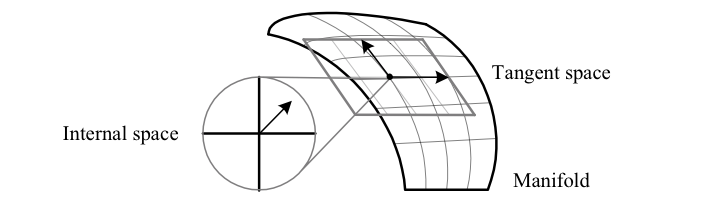
Beyond generalizing surfaces, we can generalize the properties of tangent vectors to a surface. The tangent vectors at each point of a surface lie in a two-dimensional space, a copy of \({\mathbb{R}^{2}}\) at each point. Accordingly, the tangent vectors of a general \({n}\)-dimensional differentiable manifold are defined to lie in a copy of the vector space \({\mathbb{R}^{n}}\) at each point. As we will see in subsequent chapters, the space at each point is called the tangent space, and the tangent spaces at every point taken together are called the tangent bundle. A topological manifold lacks sufficient structure to define tangents.

We can generalize the idea of tangents further by considering a new arbitrary vector space to be associated with each point of a manifold, an “internal space” that has nothing to do with tangents. This is the basic idea behind gauge theories in physics, and is best described using the language of fiber bundles.