It is important to remember that in following our intuitive picture of a Euclidean surface, our central definitions were manifolds \({M}\) and tangent vectors \({v}\). These are the “real” intrinsic objects, while their expressions in terms of a particular coordinate chart and frame are arbitrary. Coordinates and frames are “temporary” tools we use to “componentize” points and tangents on a manifold.
In particular, if a manifold is defined in terms of a set of coordinate functions that feature a singularity, this singularity may be due to the coordinates extending outside of their valid chart, telling us nothing about whether the manifold itself has a singularity. Every point of a well-defined differentiable manifold always has a local coordinate chart and tangent vectors.
For example, given the typical spherical coordinate chart for \({S^{2}}\) the associated frame will be singular at the poles, since they are outside of \({U}\) for that chart; nevertheless, tangent vectors are well-defined at these points, and can be expressed perfectly normally in a different chart.
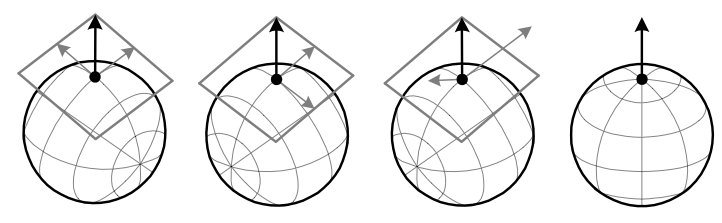
In the above figure, we see the following situations depicted:
- \({v=e_{1}+e_{2}=\partial/\partial x^{1}+\partial/\partial x^{2}}\) (expressed in a coordinate frame)
- \({v=e_{1}^{\prime}-e_{2}^{\prime}=\partial/\partial x^{\prime1}-\partial/\partial x^{\prime2}}\) (using a different coordinate frame)
- \({v=e_{1}^{\prime\prime}+3e_{2}^{\prime\prime}=\partial/\partial x^{\prime1}-\partial/\partial x^{\prime2}}\) (in a non-coordinate frame)
The final figure depicts coordinate functions that are singular at the point of interest; the manifold and vector are still well-defined, but the tangent space at this point cannot be expressed in terms of this coordinate chart.
| Δ In general, when working with objects on manifolds, it is important to keep clearly in mind whether a given symbol represents a vector, form, or function (0-form); whether any given index is a label, an abstract index or a component index in a particular frame or coordinates; and whether the object is a field with a value at each point, or is only valid at a particular point. Any calculation can always be made explicit by expressing everything in terms of functions and differential operators on them. |