In defining fiber bundles we first consider a base space (AKA basis) \({M}\) and a bundle space (AKA total space, entire space) \({E}\), which includes a surjective submersion called a bundle projection (AKA bundle submersion, projection map) \({\pi\colon E\rightarrow M}\). In the special case that \({M}\) and \({E}\) are manifolds, we require the bundle projections \({\pi}\) to be (infinitely) differentiable, and \({E}\) without any further structure is called a fibered manifold.
The space \({E}\) becomes a fiber bundle (AKA fibre bundle, bundle) if each fiber over x \({\pi^{-1}(x)}\), where \({x\in M}\), is homeomorphic to an abstract fiber (AKA standard fiber, typical fiber, fiber space, fiber) \({F}\); specifically, we must have the analog of an atlas, a collection of open trivializing neighborhoods \({\{U_{i}\}}\) that cover \({M}\), each with a local trivialization, a homeomorphism
\(\displaystyle \begin{aligned}\phi_{i}\colon\pi^{-1}(U_{i}) & \rightarrow U_{i}\times F\\ p & \mapsto\left(\pi(p),f_{i}(p)\right), \end{aligned} \)
which in a given \({\pi^{-1}(x)}\) allows us to ignore the first component and consider the last as a homeomorphism
\(\displaystyle f_{i}\colon\pi^{-1}(x)\rightarrow F. \)
This property of a bundle is described by calling it locally trivial (AKA a local product space), and if all of \({M}\) can be made a trivializing neighborhood, then \({E}\) is a trivial bundle, i.e. \({E\cong M\times F}\). The topology of a non-trivial bundle can be defined via \({E}\) itself, or imputed by the local trivializations. Note that if \({F}\) is discrete, then \({E}\) is a covering space of \({M}\), and if \({M}\) is contractible, then \({E}\) is trivial. If \({F}\) is given additional structure, \({f_{i}}\) must remain an isomorphism with respect to this structure.
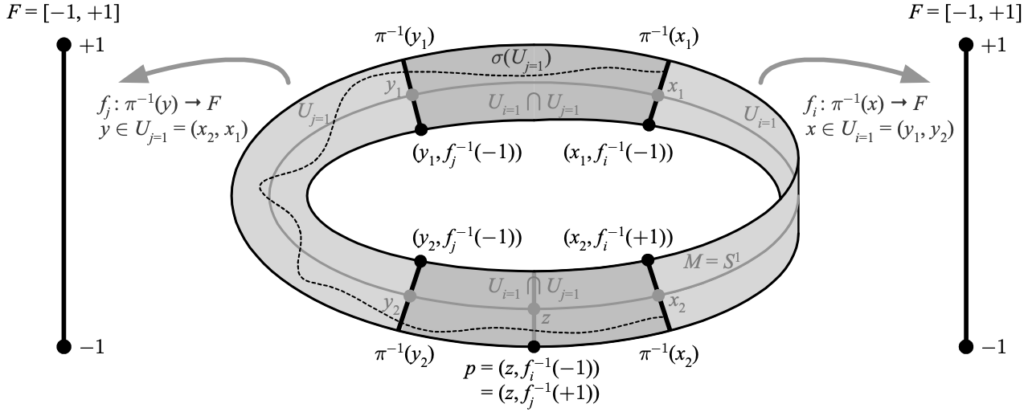
The above depicts how the Möbius strip (AKA Möbius band) has a base space which is a circle \({M=S^{1}}\), a fiber which is a line segment \({F=\left[-1,+1\right]}\), and is non-trivial, since it requires at least two trivializing neighborhoods \({U_{1}}\) and \({U_{2}}\). In the figure, the fiber over \({z}\) has two different descriptions under the two local trivializations, and a local section \({\sigma}\) (defined below) is depicted.
| Δ Fiber bundles are denoted by various combination of components and maps in various orders, frequently \({(E,M,F)}\), \({(E,M,\pi)}\), or \({(E,M,\pi,F)}\). Other notations include \({\pi\colon E\rightarrow M}\) and \({F\longrightarrow E\overset{\pi}{\longrightarrow}M}\) or just \({F\longrightarrow E\overset{}{\longrightarrow}M}\). |
| Δ The distinction between the fiber and the fiber over \({x}\) is sometimes not made clear; it is important to remember that the abstract fiber \({F}\) is not part of the bundle space \({E}\). |
| Δ A fibration is a topological structure similar to a fiber bundle whose definition (which we omit) implies that the fibers are homotopy equivalent instead of homeomorphic. For our purposes, the important fact is that every fiber bundle over a manifold is a fibration, but a fibration may not be a fiber bundle. |
A bundle map (AKA bundle morphism) is a pair of maps \({\Phi_{E}\colon E\rightarrow E^{\prime}}\) and \({\Phi_{M}\colon M\rightarrow M^{\prime}}\) between bundles that map fibers to fibers, i.e. \({\pi^{\prime}(\Phi_{E}(p))=\Phi_{M}(\pi(p))}\). Note that if \({\Phi_{M}}\) is the identity map, the bundles are over the same base space \({M}\) and this reduces to a single map satisfying \({\pi^{\prime}(\Phi(p))=\pi(p)}\).
A section (AKA cross section) of a fiber bundle is a continuous map \({\sigma\colon M\rightarrow E}\) that satisfies \({\pi(\sigma(x))=x}\). At a point \({x\in M}\) a local section always exists, being only defined in a neighborhood of \({x}\); however global sections may not exist.
| Δ It is important to remember that the base space \({M}\) is not part of the bundle space \({E}\). In particular, since a global section may not exist, the base space cannot in general be viewed as being embedded in the bundle space, and even when it can be, such an embedding is in general arbitrary. An exception is when there is a canonical global section, for example the zero section as depicted in the Möbius strip above (and in a vector bundle in general). |
The fibers of a fiber bundle (or a fibered manifold) are leaves of a foliation, but the converse is not true since the definition is only local (e.g. leaves may not be diffeomorphic, or may be submanifolds but not embedded). An example is the Möbius strip depicted above, which can be foliated by circles, but is not a circle bundle.