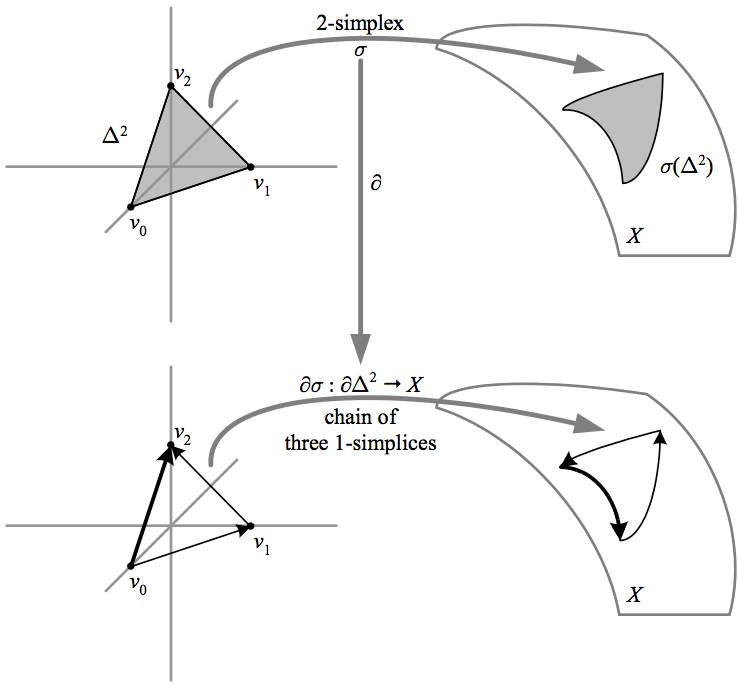
As a tool for measuring “holes” in the next section, we will need to construct \({n}\)-dimensional surfaces within a space. We will build these surfaces out of simple triangular pieces called simplices. The idea is to map triangles to the space, then build surfaces out of these triangles within the space.
- Standard n-simplex \({\Delta^{n}}\): the \({n}\)-dimensional space defined by the join of the \({(n+1)}\) unit points in \({\mathbb{R}^{n+1}}\)
- Singular n-simplex (AKA \({n}\)-simplex): a mapping \({\sigma\colon\Delta^{n}\to X}\) of the standard \({n}\)-simplex into \({X}\), the space being studied; the map is only assumed to be continuous (and so may be singular)
- n-chain: an element of \({C_{n}(X)}\), defined to be the free abelian group with basis the n-simplices \({\sigma_{\alpha}}\); i.e. the abelian group of finite formal linear sums (“chains”) \({\sum a_{\alpha}\sigma_{\alpha}}\) with coefficients \({a_{\alpha}\in\mathbb{Z}}\)
- Boundary homomorphisms \({\partial_{n}\colon C_{n}\left(X\right)\to C_{n-1}\left(X\right)}\): takes an \({n}\)-chain to the \({(n-1)}\)-chain consisting of the oriented sum of boundaries; also denoted simply \({\partial}\)
By oriented sum, it is meant that we desire a coherent orientation in \({X}\); i.e. the boundary of a boundary should vanish. We can achieve this in any dimension by taking the boundaries \({\partial\Delta^{n}}\) as oriented according to vertex order, and then defining \({\partial\sigma\left(\partial\Delta^{n}\right)\equiv\sum\left(-1\right)^{i}\sigma\left[\Delta^{n}-v_{i}\right]}\). This formalism has the effect of reversing the “backwards” boundaries by preceding them with a minus sign, as can be seen with the heavier weight arrows in the preceding figure for a 2-simplex. For 0-simplices, we define \({\partial_{0}\sigma=0}\).