If we take the exterior covariant derivative of the curvature, we get

\(\displaystyle \mathrm{D}\check{R}=0. \)

This is called the second (AKA differential) Bianchi identity, and can be verified algebraically from the definition of \({\check{R}}\). We can write this identity more explicitly as

\begin{aligned}0 & =\mathrm{D}\check{R}(u,v,w)\vec{a}\\ & =\nabla_{u}\check{R}(v,w)\vec{a}+\nabla_{v}\check{R}(w,u)\vec{a}+\nabla_{w}\check{R}(u,v)\vec{a}\\ & \phantom{{}=}-\check{R}([u,v],w)\vec{a}-\check{R}([v,w],u)\vec{a}-\check{R}([w,u],v)\vec{a}, \end{aligned}

where we have used the antisymmetry of \({\check{R}}\) and the covariant derivative acts on the value of \({\check{R}}\) as a tensor of type \({\left(1,1\right)}\). Working this expression into tensor notation and using the tensor expression for the torsion in terms of the commutator, we find that

\begin{aligned}0 & =\nabla_{e}R^{c}{}_{dab}+\nabla_{a}R^{c}{}_{dbe}+\nabla_{b}R^{c}{}_{dea}\\
& \phantom{{}=}-R^{c}{}_{dfe}T^{f}{}_{ab}-R^{c}{}_{dfa}T^{f}{}_{be}-R^{c}{}_{dfb}T^{f}{}_{ea},
\end{aligned}

or

\(\displaystyle R^{c}{}_{d[ab;e]}=R^{c}{}_{df[e}T^{f}{}_{ab]}, \)

and in the case of zero torsion, \({R^{c}{}_{d[ab;e]}=0}\).

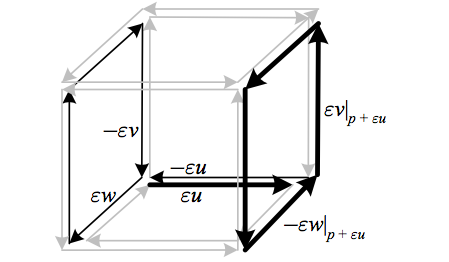
Geometrically, the second Bianchi identity can be seen as reflecting the same “boundary of a boundary” idea as that of \({\mathrm{d}^{2}=0}\) when considering the exterior derivative of a 2-form, except that here we are parallel transporting a vector \({\vec{a}}\) around each face that makes up the boundary of the cube. As in the previous section, we can take advantage of the fact that \({\check{R}(v,w)\vec{a}}\) only depends upon the local value of \({\vec{a}}\), constructing its vector field values such that e.g. \({\vec{a}\left|_{p+\varepsilon u}\right.=\parallel_{\varepsilon u}(\vec{a}\left|_{p}\right.)}\), giving us

\begin{aligned}\varepsilon\nabla_{u}\check{R}(v,w)\vec{a} & =\check{R}(v\left|_{p+\varepsilon u}\right.,w\left|_{p+\varepsilon u}\right.)\vec{a}\left|_{p+\varepsilon u}\right.-\parallel_{\varepsilon u}\check{R}(v,w)\parallel_{\varepsilon u}^{-1}\vec{a}\left|_{p+\varepsilon u}\right.\\
& =\check{R}(v\left|_{p+\varepsilon u}\right.,w\left|_{p+\varepsilon u}\right.)\parallel_{\varepsilon u}\vec{a}-\parallel_{\varepsilon u}\check{R}(v,w)\vec{a}.
\end{aligned}

The first term parallel transports \({\vec{a}}\) along \({\varepsilon u}\) and then around the parallelogram defined by \({v}\) and \({w}\) at \({p+\varepsilon u}\), while the second parallel transports \({\vec{a}}\) around the parallelogram defined by \({v}\) and \({w}\) at \({p}\), then along \({\varepsilon u}\). Thus in the case of vanishing torsion (and thus vanishing Lie commutators), we construct a cube from the vector fields \({u}\), \({v}\), and \({w}\), and find that the second Bianchi identity reflects the fact that \({\mathrm{D}\check{R}(u,v,w)\vec{a}}\) parallel transports \({\vec{a}}\) along each edge of the cube an equal number of times in opposite directions, thus canceling out any changes.

The above depicts how the second Bianchi identity reflects the fact that for vanishing torsion, \({\mathrm{D}\check{R}(u,v,w)\vec{a}}\) parallel transports \({\vec{a}}\) along each edge of the cube made of the three vector field arguments an equal number of times in opposite directions, thus canceling out any changes. Above, \({\varepsilon\nabla_{u}\check{R}(v,w)\vec{a}=\check{R}(v\left|_{p+\varepsilon u}\right.,w\left|_{p+\varepsilon u}\right.)\parallel_{\varepsilon u}\vec{a}-\parallel_{\varepsilon u}\check{R}(v,w)\vec{a}}\) is highlighted by the bold arrows representing the path along which \({\vec{a}}\) is parallel transported in the first term, and by the remaining dark arrows representing the path along which \({\vec{a}}\) is parallel transported in the second term.

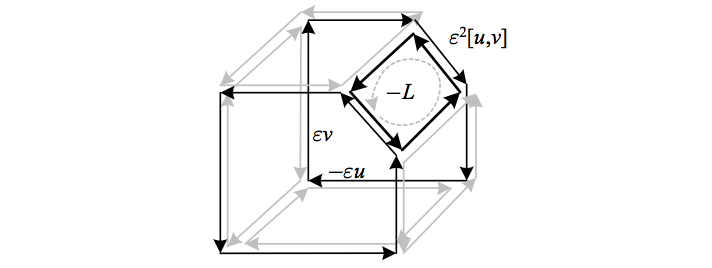
In the case of non-vanishing torsion, where there is a non-vanishing commutator \({\vec{T}(u,v)=-[u,v]\neq0}\), we find that the cube gains a “shaved edge,” and that the extra non-vanishing term \({-\check{R}([u,v],w)\vec{a}}\) in \({\mathrm{D}\check{R}}\) maintains the “boundary of a boundary” logic by adding a loop of parallel transports of \({\vec{a}}\) in the proper direction around the new “face” created.

The above depicts how in the case of a non-vanishing torsion and thus commutator, the extra term \({-\check{R}([u,v],w)\vec{a}}\) in \({\mathrm{D}\check{R}}\) maintains the cancellation of face boundaries by adding a loop \({L}\) around the new “shaved edge” created.