Recall that the Lie derivative of a vector field \({L_{v}w}\) compares the value of \({w}\) to its value after being “transported” by the local flow of \({v}\). Having defined the parallel transporter, we can now consider the covariant derivative
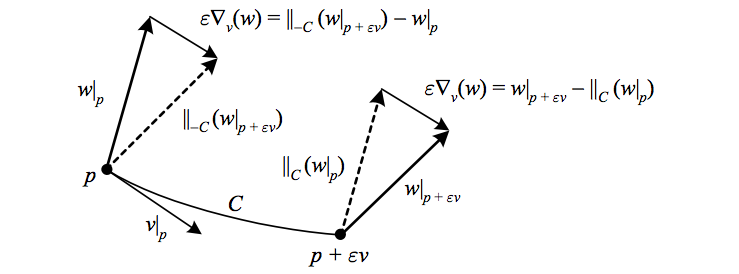
\begin{aligned}\nabla_{v}w & \equiv\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left(w\left|_{p+\varepsilon v}\right.-\parallel_{C}\left(w\left|_{p}\right.\right)\right)\\ & =\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left(\parallel_{-C}\left(w\left|_{p+\varepsilon v}\right.\right)-w\left|_{p}\right.\right), \end{aligned}
where \({C}\) is an infinitesimal curve starting at \({p}\) with tangent \({v}\). At a point \({p}\), \({\nabla_{v}w}\) then compares the value of \({w}\) at \({p+\varepsilon v}\) to its value at \({p}\) after being parallel transported to \({p+\varepsilon v}\), or equivalently in the limit \({\varepsilon\rightarrow0}\), the value of \({w}\) at \({p}\) to its value at \({p+\varepsilon v}\) after being parallel transported back to \({p}\). Recall from the section on tangent vectors that \({p+\varepsilon v}\) is well-defined in the limit \({\varepsilon\rightarrow0}\).
The above depicts how the covariant derivative \({\nabla_{v}w}\) is the difference between a vector field \({w}\) and its parallel transport in the direction \({v}\) (recall the figure conventions from the box after the figure on the Lie derivative).
Two properties that can be shown of \({\nabla_{v}w}\) are that it is linear in \({v}\), and that for a function \({f}\) on \({M}\) it obeys the rule \({\nabla_{v}\left(fw\right)=v\left(f\right)w+f\nabla_{v}\left(w\right)}\). As we will see, this is the Leibniz rule for the covariant derivative generalized to the tensor algebra. Note that \({\nabla_{v}w}\) is a directional derivative, i.e. it depends only upon the value of \({v}\) at \({p}\); \({v}\) is in effect used only to choose a direction. In contrast, \({L_{v}w}\) requires \({v}\) to be a vector field, since \({w}\) is in this case compared to its value after being “transported” by the local flow of \({v}\), and so depends on the derivative of \({v}\) at \({p}\).
| Δ It is important to remember that there is no way to “transport” a vector on a manifold without introducing some extra structure. In particular, recall that the exterior derivative does not compare vectors at all. |
Instead of parallel transport, one can consider the covariant derivative as the fundamental structure being added to the manifold. In this case it is useful to define the covariant derivative along a smooth parametrized curve \({C(t)}\) by using the tangent to the curve as the direction, i.e.
\(\displaystyle \frac{\mathrm{D}}{\mathrm{d}t}w\equiv\mathrm{D}_{t}w\equiv\nabla_{\dot{C}(t)}w, \)
where \({\dot{C}(t)}\) is the tangent to \({C}\) at \({t}\). \({\mathrm{D}_{t}w}\) is sometimes called the absolute derivative (AKA intrinsic derivative) and its definition only requires that \({w}\) be defined along the curve \({C(t)}\). We can then define the parallel transport of \({w\left|_{p}\right.}\) along \({C(t)}\) as the vector field \({w}\) that satisfies \({\mathrm{D}_{t}w=0}\) along the curve.
| Δ The notation for the absolute derivative is potentially confusing since the implicitly referenced curve \({C(t)}\) does not appear in the expression \({\mathrm{D}_{t}w}\). |