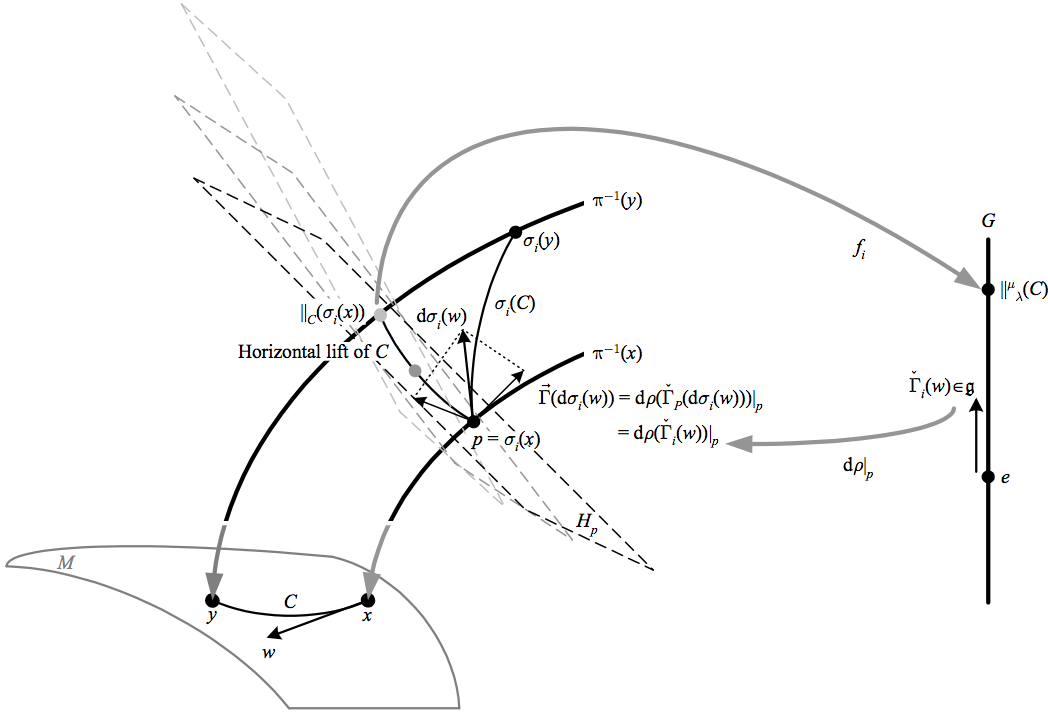
On any smooth bundle with connection, we consider the horizontal tangent space to define the direction of parallel transport. More precisely, we define a horizontal lift of a curve \({C}\) from \({x}\) to \({y}\) on \({M}\) to be a curve \({C_{p}}\) that starts at \({p\in\pi^{-1}(x)}\), projects down to \({C}\), and has tangents which are all horizontal:
\(\displaystyle \begin{aligned}\pi\left(C_{p}\right) & =C\\ \dot{C}_{p}\left|_{q}\right. & \in H_{q} \end{aligned} \)
The horizontal lift \({C_{p}}\) is unique for each \({p\in\pi^{-1}(x)}\), and the endpoints of all such lifts let us define the bundle parallel transporter
\(\displaystyle \parallel_{C}\colon\pi^{-1}(x)\rightarrow\pi^{-1}(y), \)
which is a diffeomorphism between fibers.
On a frame bundle \({(P=F(E),M,\pi,GL(n,\mathbb{K}))}\) with connection, the bundle parallel transporter commutes with the right action:
\(\displaystyle \parallel_{C}\left(g\left(p\right)\right)=g\left(\parallel_{C}\left(p\right)\right) \)
We can then recover the parallel transporter on \({M}\) by choosing a frame (i.e. a local trivialization), using the horizontal lift that starts at the element \({\sigma_{i}=e_{i}}\) in the identity section, and recalling the relation \({e_{p}=e_{i}f_{i}(p)}\):
\(\displaystyle \begin{aligned}\parallel_{C}\left(e_{i}\left|_{x}\right.\right) & =e_{i}\left|_{y}\right.f_{i}\left(\parallel_{C}\left(e_{i}\left|_{x}\right.\right)\right)\\ \Rightarrow\left(\parallel_{C}\left(v\right)\right)_{i}^{\mu}\left|_{y}\right. & =f_{i}\left(\parallel_{C}\left(e_{i}\left|_{x}\right.\right)\right)^{\mu}{}_{\lambda}v_{i}^{\lambda}\left|_{x}\right.\\ \Rightarrow\parallel^{\mu}{}_{\lambda}\left(C\right) & =f_{i}\left(\parallel_{C}\left(e_{i}\left|_{x}\right.\right)\right)^{\mu}{}_{\lambda} \end{aligned} \)
The second line transforms vector components using the change of basis matrix in the opposite direction.
Similarly, on the frame bundle we can recover the connection 1-form on \({v\in T_{x}M}\) within a trivializing neighborhood by using the pullback of the identity section to arrive at
\(\displaystyle \begin{aligned}\check{\Gamma}_{i}(v) & =\sigma_{i}^{*}\check{\Gamma}_{P}(v)\\ & =\check{\Gamma}_{P}\left(\mathrm{d}\sigma_{i}(v)\right), \end{aligned} \)
where to avoid clutter we write \({\check{\Gamma}_{i}}\) instead of \({\left(\check{\Gamma}_{A}\right)_{i}}\). On \({F(E)}\), \({\sigma_{i}=e_{i}}\) is the frame used to define the components of vectors in the internal space on \({U_{i}}\), and \({\check{\Gamma}_{i}(v)}\) then is the element of \({gl(n,\mathbb{K})}\) corresponding to the vertical component of \({v}\) after being mapped to a tangent of the identity section. Thus since we consider the horizontal tangent space to define the direction of parallel transport, \({\check{\Gamma}_{i}(v)}\) is the infinitesimal linear transformation that takes the parallel transported frame to the frame in the direction \({v}\), the same interpretation as we found for the parallel transporter on manifolds.
| Δ It is important to remember that \({\check{\Gamma}_{i}}\) takes values that are dependent upon the local trivialization that defines the identity section (i.e. it is frame-dependent), while the values of \({\check{\Gamma}_{P}}\) are intrinsic to the frame bundle. This reflects the fact that the connection is a choice of horizontal correspondences between frames, and so cannot have any value intrinsic to \({E}\). |
The above depicts how a principal connection 1-form on \({(P,M,G)}\) defines the vertical component of its argument as a value in the Lie algebra \({\mathfrak{g}}\) via the isomorphism defined by the differential of the right action \({\mathrm{d}\rho}\). A horizontal lift of a curve \({C}\) yields the parallel transporter, and the pullback by the identity section recovers the connection 1-form on \({M}\).
The transition functions on the frame bundle can be viewed as \({GL(n,\mathbb{K})}\)-valued 0-forms \({\check{g}_{ij}}\) on \({U_{i}\cap U_{j}}\), and it can be shown that
\(\displaystyle \check{\Gamma}_{i}(v)=\check{g}_{ij}\check{\Gamma}_{j}(v)\check{g}_{ij}^{-1}+\check{g}_{ij}\mathrm{d}\check{g}_{ij}^{-1}(v), \)
which is the transformation of the connection 1-form under a change of frame \({\check{g}_{ij}^{-1}}\) from the section on manifold connections. This is consistent with the interpretation of the action of \({g_{ij}}\) as a change of frame \({g_{ij}^{-1}}\) in the section on vector bundles, and it can be shown that a unique connection on \({F(E)}\) is determined by locally defined connection 1-forms on \({M}\) and sections that are related by the same transition functions.
| ◊ The inhomogeneous transformation of the connection 1-form can be viewed as reflecting the fact that both the location and “shape” of the identity section is different across local trivializations (although we have depicted the identity sections as “flat,” the values of each \({\sigma_{i}(x)}\) are smooth but arbitrary). |
| ◊ This demonstrates the advantage of the principal bundle formulation, in that the connection 1-form on \({M}\) is frame-dependent, and therefore cannot in general be defined on all of \({M}\), while in contrast the principal connection 1-form is defined on all of \({F(E)}\), and can be used to determine a consistent connection 1-form on \({M}\) within each trivializing neighborhood. |
Under either type of gauge transformation, it can also be shown that as expected we have
\(\displaystyle \check{\Gamma}_{i}^{\prime}(v)=\check{\gamma}_{i}\check{\Gamma}_{i}(v)\check{\gamma}_{i}^{-1}+\check{\gamma}_{i}\mathrm{d}\check{\gamma}_{i}^{-1}(v). \)