The extension of the coordinate-free definition of \({\mathrm{d}}\) to general \({k}\)-forms gives the expression

\begin{aligned} \mathrm{d}\varphi\left(v_{0},\dotsc,v_{k}\right) & \equiv\sum_{j=0}^{k}\left(-1\right)^{j}v_{j}\left(\varphi\left(v_{0},\dotsc,v_{j-1},v_{j+1},\dotsc,v_{k}\right)\right)\\
& \phantom{{}=}+\sum_{i<j}\left(-1\right)^{i+j}\varphi\left(\left[v_{i},v_{j}\right],v_{0},\dotsc,v_{i-1},v_{i+1},\dotsc,v_{j-1},v_{j+1},\dotsc,v_{k}\right).
\end{aligned}

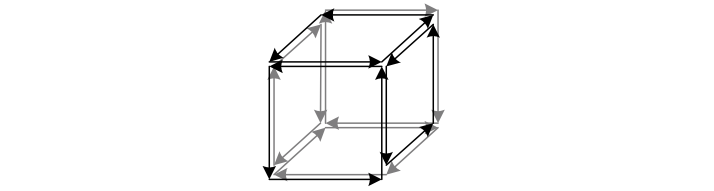
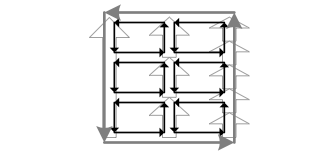
Our picture for \({1}\)-forms then extends to higher dimensions using much the same reasoning as used in the section on homology. For example, assuming vanishing Lie brackets to simplify the picture, the exterior derivative of a 2-form \({\mathrm{d}\varphi\left(u,v,w\right)}\) can be viewed as the “sum of \({\varphi}\) on the boundary faces of the cube defined by its arguments.” If \({\varphi=\mathrm{d}\psi\left(v,w\right)}\) is the boundary of a face, \({\mathrm{d}\varphi=\mathrm{d}^{2}\psi}\) is the sum of the boundaries of the faces; each edge is then counted by two faces with opposite signs, thus canceling so that again we have \({\mathrm{d}^{2}=0}\).

The above depicts a 3-form \({\mathrm{d}\varphi=\mathrm{d}^{2}\psi}\) summing \({\psi}\) over the edges of the faces of a cube. The sum vanishes since each edge is counted twice with opposite signs.

The similarity between the exterior derivative \({\mathrm{d}}\) and the boundary homomorphism \({\partial}\) from homology is no illusion, as we will see shortly in the section Homology on Manifolds.

In a holonomic frame, we can obtain an expression for \({\mathrm{d}\varphi}\) in terms of coordinates

\begin{aligned}\mathrm{d}\varphi & =\sum_{\mu_{0}<\dotsb<\mu_{k}}\left(\sum_{j=0}^{k}\left(-1\right)^{j}\frac{\partial}{\partial x^{\mu_{j}}}\varphi_{\mu_{0}\dots\mu_{j-1}\mu_{j+1}\dots\mu_{k}}\right)\mathrm{d}x^{\mu_{0}}\wedge\dotsb\wedge\mathrm{d}x^{\mu_{k}}\\
& =\frac{\partial}{\partial x^{\mu_{0}}}\varphi_{\mu_{1}\dots\mu_{k}}\mathrm{d}x^{\mu_{0}}\wedge\dotsb\wedge\mathrm{d}x^{\mu_{k}}\\
& =\frac{\partial\varphi_{I}}{\partial x^{\mu_{0}}}\mathrm{d}x^{\mu_{0}}\wedge\mathrm{d}x^{I},
\end{aligned}

so that in terms of array components we have

\begin{aligned}\left(\mathrm{d}\varphi\right)_{\mu_{0}\dots\mu_{k}} & =\sum_{j=0}^{k}\left(-1\right)^{j}\frac{\partial}{\partial x^{\mu_{j}}}\varphi_{\mu_{0}\dots\mu_{j-1}\mu_{j+1}\dots\mu_{k}}.\end{aligned}

It is not hard to see that the exterior derivative commutes with the pullback, i.e. \({\Phi^{*}\mathrm{d}\varphi=\mathrm{d}\Phi^{*}\varphi}\).

If we include an inner product, vector calculus can be seen to correspond to exterior calculus on \({\mathbb{R}^{3}}\), and can thus be generalized to arbitrary dimensions:

• For a function (0-form) \({f}\), the components of the 1-form \({\mathrm{d}f}\) correspond to those of the gradient of \({f}\), i.e. \({(\mathrm{d}f)_{\mu}=(\nabla f)^{\mu}}\) or \({\nabla f=(\mathrm{d}f)^{\sharp}}\); a generalization of the gradient is then the 1-form \({\mathrm{d}f}\)
• For a 1-form with components equal to those of a vector \({\varphi_{\mu}=v^{\mu}}\), the components of \({\mathrm{d}\varphi}\) correspond to those of the curl of \({v}\), i.e. \({(\mathrm{d}\varphi)_{\mu}=(\nabla\times v)^{\mu}}\) or \({(\nabla\times v)=(*\mathrm{d}(v^{\flat}))^{\sharp}}\); a generalization of the curl is then the 2-form \({\mathrm{d}\varphi}\)
• For a 2-form with components equal to those of a vector \({\psi_{\mu}=(*\varphi)_{\mu}=v^{\mu}}\), the value of \({\mathrm{d}\psi}\) corresponds to the value of the divergence of \({v}\), i.e. \({\mathrm{d}\psi=\nabla\cdot v}\) or \({\nabla\cdot v=*\mathrm{d}(*(v^{\flat}))}\); a generalization of the divergence is then the value \({*\mathrm{d}(*\varphi)}\)

In \({\mathbb{R}^{3}}\) the relations curl grad = div curl = 0 thus correspond to the property \({\mathrm{d}^{2}=0}\). Note that we have used the musical isomorphisms on \({\mathbb{R}^{3}}\), which imply an inner product, as does the Hodge star. These generalizations can be extended to a pseudo inner product with signature \({\left(r,s\right)}\) by defining the divergence as \({(-1)^{s}*\mathrm{d}(*v^{\flat})}\), which is then independent of both signature and orientation.

Finally, the classical gradient, curl, and divergence integral theorems in vector calculus are generalized to Stokes’ theorem: for an \({(n-1)}\)-form \({\varphi}\) on a compact oriented manifold \({M^{n}}\) with boundary \({\partial M}\),

\(\displaystyle \int_{M}\,\mathrm{d}\varphi=\int_{\partial M}\varphi. \)

This is essentially the integral form of the property \({\mathrm{d}^{2}=0}\): summing \({\mathrm{d}\varphi}\) over \({M}\) can be pictured as summing \({\varphi}\) over the boundaries of infinitesimal volumes, so that all internal boundaries cancel and what is left is \({\varphi}\) over the outer boundary \({\partial M}\).

We will not address the details of defining integration on manifolds here, but the basic idea is relatively straightforward: a coordinate chart maps an \({n}\)-dimensional sub-manifold \({U}\) of \({M^{n}}\) to \({S\in\mathbb{R}^{n}}\); an \({n}\)-form \({\varphi}\) can then be written \({f(x_{I})\,\mathrm{d}x^{I}}\), and its integral over \({U}\) is defined to be \({\int_{S}f(x_{I})\,\mathrm{d}x^{I}}\), which can be shown to be coordinate-independent. Note that without additional structure on the manifold, we cannot integrate functions or other forms over \({M^{n}}\) besides \({n}\)-forms (or pseudo \({n}\)-forms if \({U}\) is non-orientable).

We can further generalize the divergence to \({k}\)-forms \({\varphi}\) by defining the codifferential (AKA coderivative, exterior coderivative)

\begin{aligned}\delta\varphi & \equiv(-1)^{k}*^{-1}\mathrm{d}(*\varphi)\\
& =(-1)^{n(k+1)+s+1}*\mathrm{d}(*\varphi)\\
\Rightarrow\mathrm{div}\left(v\right) & =-\delta v^{\flat}.
\end{aligned}

The map \({\delta:\Lambda^{k}M\to\Lambda^{k-1}M}\) does not follow the Leibniz rule and so is not a derivation. However, we do have \({\delta^{2}=0}\), so that we may write \({\Delta\equiv\left(\mathrm{d}+\delta\right)^{2}=\mathrm{d}\delta+\delta\mathrm{d}}\), which (usually for \({s=0}\)) is called the Laplace-Beltrami operator (AKA Laplace operator, Laplacian, Laplace–de Rham operator); a form on a Riemannian manifold for which it vanishes is called a harmonic form. For \({f\in\Lambda^{0}M}\) we have \({\delta f=0}\) and \({\Delta f=-\mathrm{div}\left(\nabla f\right)}\); on a flat Lorentzian manifold in the mostly pluses signature its negative is denoted \({\square f\equiv\partial^{\mu}\partial_{\mu}f=-\partial_{t}^{2}f+\Delta f}\), where \({\square}\) is called the d’Alembertian (AKA d’Alembert operator, wave operator, box operator), whose spatial part despite the opposite sign is denoted \({\Delta f\equiv\nabla^{2}f\equiv\nabla\cdot\nabla f=\partial_{x}^{2}f+\partial_{y}^{2}f+\partial_{z}^{2}f}\) and called the Laplacian (AKA Laplace operator). \({\Delta f=0}\) is then called Laplace’s equation, while a fixed \({\rho\in\Lambda^{0}M}\) defines Poisson’s equation \({\Delta f=\rho}\).

If \({\varphi\in\Lambda^{k}M}\) and \({\psi\in\Lambda^{k+1}M}\) so that \({\mathrm{d}\left(\varphi\wedge*\psi\right)\in\Lambda^{n}M}\), it is not hard to see that

\(\displaystyle \int_{\partial M}\left(\varphi\wedge*\psi\right)=\int_{M}\left\langle \mathrm{d}\varphi,\psi\right\rangle\Omega -\left\langle \varphi,\delta\psi\right\rangle\Omega, \)

which means that if \({\varphi\wedge*\psi}\) vanishes on \({\partial M}\) (or \({\partial M=0}\)) we have \({\int_{M}\left\langle \mathrm{d}\varphi,\psi\right\rangle \Omega=\int_{M}\left\langle \varphi,\delta\psi\right\rangle \Omega}\). In particular, for \({f\in\Lambda^{0}M}\) and \({v^{\flat}\in\Lambda^{1}M}\), we have

\(\displaystyle \int_{\partial M}f\left(*v^{\flat}\right) =\int_{M}\left\langle \nabla f,v\right\rangle \Omega+f\mathrm{div}\left(v\right)\Omega, \)

or for \({f=1}\) and recalling that \({i_{v}\Omega=*(v^{\flat})}\),

\begin{aligned}\int_{\partial M}*v^{\flat} & =\int_{M}\mathrm{div}\left(v\right)\Omega\\
\Rightarrow\int_{M}\mathrm{div}\left(v\right)\Omega & =\int_{\partial M}i_{v}\Omega\\ &
=\int_{\partial M}\left\langle v,\hat{n}\right\rangle i_{\hat{n}}\Omega,\end{aligned}

where \({\hat{n}}\) is the unit normal vector to \({\partial M}\), the classical divergence theorem (AKA Gauss’s theorem, Ostrogradsky’s theorem).