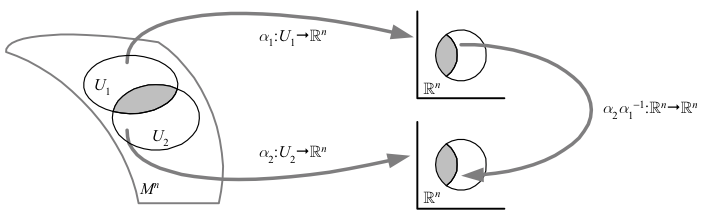
Recall that the key feature of a topological manifold \({M^{n}}\) is that every point has an open neighborhood homeomorphic to an open subset of \({\mathbb{R}^{n}}\). To make this precise we define the following terms.
- Coordinate chart (AKA parameterization, patch): a homeomorphism \({\alpha\colon U\to\mathbb{R}^{n}}\) from an open set \({U\subset M^{n}}\) to an open subset of \({\mathbb{R}^{n}}\)
- Coordinate functions (AKA coordinates): the maps \({a^{\mu}\colon U\to\mathbb{R}}\) that project \({\alpha}\) down to one of the canonical Cartesian components
- Atlas: a collection of coordinate charts that cover the manifold
- Coordinate transformation (AKA change of coordinates, transition function): in a region covered by two charts, we can construct the map \({\alpha_{2}\circ\alpha_{1}^{-1}\colon\mathbb{R}^{n}\to\mathbb{R}^{n}}\)
| Δ A coordinate chart is sometimes defined to be the inverse map \({\alpha^{-1}\colon\mathbb{R}^{n}\to M}\) valid on an open subset of \({\mathbb{R}^{n}}\), with similar changes to related definitions such as coordinate functions. |
The coordinate transformations are simply maps on Euclidean space, so we can require them to be infinitely differentiable (AKA smooth, \({C^{\infty}}\)). An atlas whose charts all have smooth coordinate transformations determines a differentiable structure, which turns the topological manifold into a differentiable manifold (AKA smooth manifold). Two differential structures are considered to be equivalent if the union of their atlases still results in smooth coordinate transformations. Unless otherwise noted, from this point forward “manifold” will mean differentiable manifold.
A complex manifold is defined to have an atlas of charts to \({\mathbb{C}^{n}}\) whose coordinate transformations are analytic. Complex \({n}\)-manifolds are a subset of real \({2n}\)-manifolds, but atlases are highly constrained since complex analytic functions are much more constrained than smooth functions. By “manifold” we will always mean a real manifold in this book.
With the addition of a differentiable structure, one can define the various tools of calculus on manifolds in a straightforward way. Differentiable functions \({f\colon U\to\mathbb{R}}\) require the map \({f\circ\alpha^{-1}\colon\mathbb{R}^{n}\to\mathbb{R}}\) to be differentiable, and differentials \({\partial/\partial a^{\mu}}\) are defined at a point \({p\in U}\) by
\(\displaystyle \left.\frac{\partial}{\partial a^{\mu}}\left(f\right)\right|_{p}\equiv\left.\frac{\partial}{\partial x^{\mu}}\left(f\circ\alpha^{-1}\left(x\right)\right)\right|_{x=\alpha(p)}. \)
where \({x\in\mathbb{R}^{n}}\). All of the usual relations of calculus hold with these definitions.
| Δ To avoid clutter, a common abuse of notation is to use \({x^{\mu}}\) to denote any or all of three quantities: the point \({p\in M}\), the coordinate functions \({a^{\mu}\colon M\to\mathbb{R}}\), and the \({\mathbb{R}^{n}}\) \({n}\)-tuplet \({x^{\mu}=a^{\mu}\left(p\right)}\). Another potential source of confusion is that \({x^{\mu}}\) is also commonly used to refer to the coordinates of a curve on \({M}\). Similarly, the differential \({\partial/\partial a^{\mu}}\) is usually denoted \({\partial/\partial x^{\mu}}\). We will follow these conventions going forward, but when dealing with fundamental definitions or pictures, it is important to distinguish these very different quantities from each other. Another shortcut is to denote differentials by \({\partial_{\mu}}\); as with basis vectors, it is important to remember that these are labels, not component indices. |