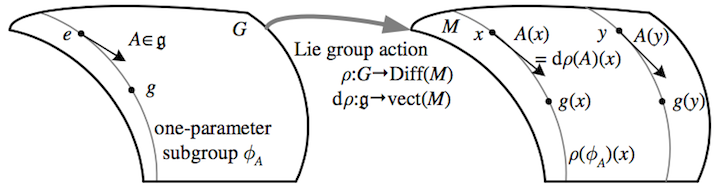
A Lie group action \({\rho}\) is a smooth homomorphism from \({G}\) to \({\textrm{Diff}(M)}\). An element of \({G}\) near the identity then moves each point of \({M}\) to a nearby point. So for any vector \({A\in\mathfrak{g}}\), the one-parameter subgroup \({\phi_{A}}\) from the identity along \({A}\) maps to a curve in \({M}\) at each point. The differential of this mapping takes \({A}\) to a vector field on \({M}\), and this relation is in fact a Lie algebra homomorphism \({\mathrm{d}\rho\colon\mathfrak{g}\to\textrm{vect}(M)}\), the corresponding Lie algebra action. Recalling the construction of the Lie derivative, we see that the Lie algebra action of \({A\in\mathfrak{g}}\), called the fundamental vector field corresponding to \({A}\), is the vector field on \({M}\) whose local flow is the Lie group action of the one-parameter subgroup \({\phi_{A}}\). If \({G}\) acts on itself by right translation, the fundamental vector fields are just the left-invariant vector fields.

In the case of a Lie group representation on a real or complex vector space \({V}\), the corresponding Lie algebra representation maps \({\mathfrak{g}}\) to a linear subalgebra of \({\textrm{vect}(V)}\) that is isomorphic to \({gl(V)}\). The Lie bracket in this case is the Lie commutator, whether viewed as that of vector fields, of transformations, or of matrices. Similarly one can show that if a Lie algebra \({\mathfrak{g}}\) has a matrix representation, and a compact connected Lie group \({G}\) corresponds to \({\mathfrak{g}}\), then \({G}\) has a matrix representation given by the matrix exponential of the Lie algebra representation.

Every finite-dimensional real Lie algebra has a faithful finite-dimensional real representation, i.e. can be viewed as a class of real matrices. This result is a special case of two theorems dealing with scalars in more general fields, Ado’s theorem and Iwasawa’s theorem. The analog is not true in general for finite-dimensional Lie groups, although most Lie groups used in physics can be viewed as matrix groups. A standard counter-example given is the universal covering group of \({SL(2,\mathbb{R})}\), which is infinite-sheeted and therefore has no faithful finite-dimensional representation.