A smooth bundle \({(E,M,\pi)}\) is a manifold itself, and thus has tangent vectors. A tangent vector \({v}\) at \({p\in E}\) is called a vertical tangent if \({\mathrm{d}\pi(v)=0}\), i.e. if it is tangent to the fiber over \({x}\) where \({\pi(p)=x}\), so the projection down to the base space vanishes. The vertical tangent space \({V_{p}}\) is then the subspace of the tangent space \({T_{p}}\) at \({p}\) consisting of vertical tangents, and viewing the vertical tangent spaces as fibers over \({E}\) we can form the vertical bundle \({(VE,E,\pi_{V})}\), which is a subbundle of \({TE}\). We can also consider differential forms on a smooth bundle, which take arguments that are tangent vectors on \({E}\). A form is called a horizontal form if it vanishes whenever any of its arguments are vertical.

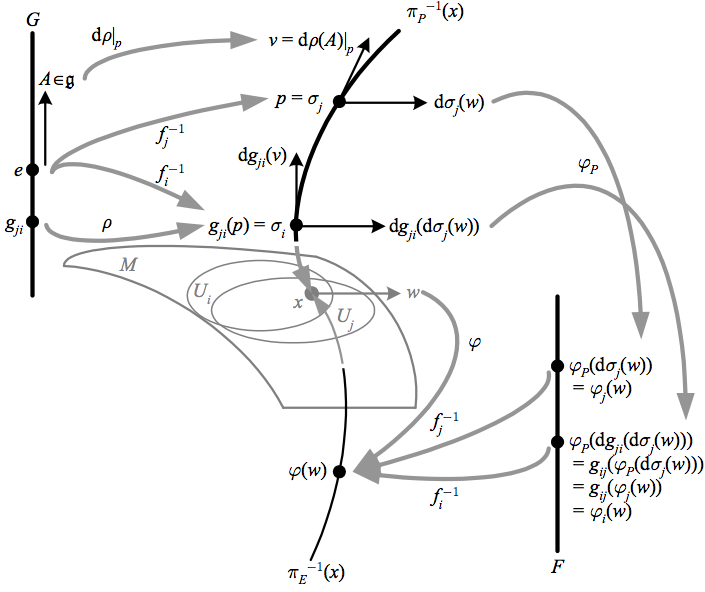
On a smooth principal bundle \({(P,M,G)}\), we have a consistent right action \({\rho\colon G\rightarrow\mathrm{Diff}(P)}\), and the corresponding Lie algebra action \({\mathrm{d}\rho\colon\mathfrak{g}\rightarrow\mathrm{vect}(P)}\) is then a Lie algebra homomorphism. The fundamental vector fields corresponding to elements of \({\mathfrak{g}}\) are vertical tangent fields; in fact, at a point \({p}\), \({\mathrm{d}\rho\left|_{p}\right.}\) is a vector space isomorphism from \({\mathfrak{g}}\) to \({V_{p}}\):

\(\displaystyle \mathrm{d}\rho\left|_{p}\right.\colon\mathfrak{g}\overset{\cong}{\rightarrow}V_{p} \)

In addition, the right action \({g\colon P\rightarrow P}\) of a given element \({g}\) corresponds to a right action \({\mathrm{d}g\colon TP\rightarrow TP}\), which maps tangent vectors on \({P}\) via

\(\displaystyle \mathrm{d}g(v)\colon T_{p}P\rightarrow T_{g(p)}P. \)

This map is an automorphism of \({TP}\) restricted to \({\pi_{P}^{-1}(x)}\), which we denote \({T_{\pi^{-1}(x)}P}\), and it preserves vertical tangent vectors. We can then consider the pullback \({g^{*}\varphi(v_{1},\ldots,v_{k})=\varphi(\mathrm{d}g(v_{1}),\ldots,\mathrm{d}g(v_{k}))}\) as a right action on the space \({\Lambda^{k}P}\) of \({k}\)-forms on \({P}\).

If we have a bundle \({(E,M,\pi_{E},F)}\) associated to \({(P,M,\pi_{P},G)}\), we can define an \({F}\)-valued form \({\varphi_{P}}\), which can be viewed on each \({\pi_{P}^{-1}(x)}\) as a mapping

\(\displaystyle \varphi_{P}\colon T_{\pi^{-1}(x)}P\otimes\cdots\otimes T_{\pi^{-1}(x)}P\rightarrow F\times\pi_{P}^{-1}(x), \)

where \({g\in G}\) has a right action \({\mathrm{d}g}\) on \({T_{\pi^{-1}(x)}P}\) and a left action \({g}\) on the abstract fiber \({F}\) of \({E}\). The form \({\varphi_{P}}\) is called an equivariant form if this mapping is equivariant with respect to these actions, i.e. if

\(\displaystyle g^{*}\varphi_{P}=g^{-1}\left(\varphi_{P}\right). \)

If \({\varphi_{P}}\) is also horizontal, then it is called a horizontal equivariant form (AKA basic form, tensorial form). If we pull back a horizontal equivariant form to the base space \({M}\) using the identity sections, we get forms

\(\displaystyle \varphi_{i}\equiv\sigma_{i}^{*}\varphi_{P} \)

on each \({U_{i}\subset M}\). Using the identity section relation \({\sigma_{i}=g_{ij}^{-1}(\sigma_{j})}\) and the pullback composition property \({\left(g(h)\right)^{*}\varphi=h^{*}\left(g^{*}\varphi\right)}\), we see that the values of these forms satisfy

\(\displaystyle \begin{aligned}\varphi_{i} & =\left(g_{ij}^{-1}(\sigma_{j})\right)^{*}\varphi_{P}\\ & =\sigma_{j}^{*}\left(\left(g_{ij}^{-1}\right)^{*}\varphi_{P}\right)\\ & =\sigma_{j}^{*}\left(g_{ij}\left(\varphi_{P}\right)\right)\\ & =g_{ij}\left(\varphi_{j}\right), \end{aligned} \)

where in the third line \({g_{ij}}\) is acting on the value of \({\varphi_{P}}\). This means that at a point \({x}\) in \({U_{i}\cap U_{j}}\), the values of \({\varphi_{i}}\) and \({\varphi_{j}}\) in the abstract fiber \({F}\) correspond to a single point in \({\pi_{E}^{-1}(x)\in E}\), so that the union \({\bigcup\varphi_{i}}\) can be viewed as comprising a single \({E}\)-valued form \({\varphi}\) on \({M}\). Such a form is sometimes called a section-valued form, since for fixed argument vector fields its value on \({M}\) is a section of \({E}\). It can be shown that the correspondence between the \({E}\)-valued forms \({\varphi}\) on \({M}\) and the horizontal equivariant \({F}\)-valued forms on \({P}\) is one-to-one. Equivariant \({F}\)-valued 0-forms on \({P}\) are automatically horizontal (since one cannot pass in a vertical argument), and are thus one-to-one with sections on \({E}\).

The above depicts how the differential of the right action of \({G}\) on \({\pi_{P}^{-1}(x)\in P}\) creates an isomorphism to the vertical tangent space \({\mathfrak{g}\cong V_{p}}\). A horizontal equivariant form \({\varphi_{P}}\) on \({P}\) maps non-vertical vectors to the abstract fiber \({F}\) of an associated bundle, and pulling back by the identity sections yields an \({E}\)-valued form \({\varphi}\) on \({M}\). Although denoted identically, the \({f_{i}}\) are those corresponding to each bundle.

On the frame bundle \({(P,M,\pi_{P},GL(n,\mathbb{K}))}\) associated with a vector bundle \({(E,M,\pi_{E},\mathbb{K}^{n})}\), a \({\mathbb{K}^{n}}\)-valued form \({\vec{\varphi}_{P}}\) is then equivariant if

\(\displaystyle g^{*}\vec{\varphi}_{P}=\check{g}^{-1}\vec{\varphi}_{P}, \)

where \({\check{g}^{-1}}\) is a matrix-valued 0-form on \({P}\) operating on the \({\mathbb{K}^{n}}\)-valued form \({\vec{\varphi}_{P}}\). The pullback of a horizontal equivariant form on \({P}\) to the base space \({M}\) using the identity sections satisfies

\(\displaystyle \vec{\varphi}_{i}=\check{g}_{ij}\vec{\varphi}_{j}, \)

where \({\check{g}_{ij}}\) is now a matrix-valued 0-form on \({M}\). At a point \({x}\) in \({U_{i}\cap U_{j}}\), the values of \({\vec{\varphi}_{i}}\) and \({\vec{\varphi}_{j}}\) in the abstract fiber \({\mathbb{K}^{n}}\) correspond to a single abstract vector in \({V_{x}=\pi_{E}^{-1}(x)\in E}\), so that the union \({\bigcup\vec{\varphi}_{i}}\) can be viewed as comprising a single \({V}\)-valued form \({\vec{\varphi}}\) on \({M}\). Thus an equivariant \({\mathbb{K}^{n}}\)-valued 0-form on \({P}\) is a matter field on \({M}\).

Under an automorphism gauge transformation, the transformation of a horizontal equivariant form on the frame bundle \({P}\) is defined by the pullback of the automorphism

\(\displaystyle \vec{\varphi}_{P}^{\prime}\equiv\left(\gamma^{-1}\right)^{*}\vec{\varphi}_{P}. \)

The automorphism does not give us a right action on \({T_{\pi^{-1}(x)}P}\) by a fixed element, but it does give a right action when acting on the element in the identity section, so since the identity sections remain constant we have

\begin{aligned}\vec{\varphi}_{i}^{\prime} & =\sigma_{i}^{*}\left(\gamma^{-1}\right)^{*}\vec{\varphi}_{P}\\
& =\left(\gamma^{-1}\sigma_{i}\right)^{*}\vec{\varphi}_{P}\\
& =\left(\gamma_{i}^{-1}\sigma_{i}\right)^{*}\vec{\varphi}_{P}\\
& =\sigma_{i}^{*}\left(\gamma_{i}^{-1}\right)^{*}\vec{\varphi}_{P}\\
& =\sigma_{i}^{*}\check{\gamma}_{i}\vec{\varphi}_{P}\\
& =\check{\gamma}_{i}\vec{\varphi}_{i},
\end{aligned}

where we have used \({\left(g(h)\right)^{*}\varphi=h^{*}\left(g^{*}\varphi\right)}\) twice, and in the penultimate line we used the equivariance of \({\vec{\varphi}_{P}}\). Under neighborhood-wise gauge transformations, there is no change in \({\vec{\varphi}_{P}}\) but we have new identity sections \({\sigma_{i}^{\prime}(x)=\gamma_{i}^{-1}(\sigma_{i}(x))}\), so that we get

\(\displaystyle \begin{aligned}\vec{\varphi}_{i}^{\prime} & =\sigma_{i}^{\prime*}\vec{\varphi}_{P}\\ & =\left(\gamma_{i}^{-1}\left(\sigma_{i}\right)\right)^{*}\vec{\varphi}_{P}\\ & =\sigma_{i}^{*}\left(\gamma_{i}^{-1}\right)^{*}\vec{\varphi}_{P}\\ & =\check{\gamma}_{i}\vec{\varphi}_{i}, \end{aligned} \)

matching the behavior for both automorphism gauge transformations and for gauge transformations as previously defined directly on \({M}\) in the section on matter fields.

Note that if a horizontal equivariant form takes values in the abstract fiber \({F}\) of another bundle associated to the frame bundle, the same reasoning applies, but with \({\check{\gamma}_{i}}\) applied using the left action of \({G}\) on \({F}\). In particular, recalling that the adjoint rep \({\rho=\mathrm{Ad}}\) of \({G}\) on \({\mathfrak{g}}\) defines an associated bundle \({(\mathrm{Ad}P,M,\mathfrak{g})}\) to \({P}\), we can consider a \({\mathfrak{g}}\)-valued horizontal equivariant form \({\check{\Theta}_{P}}\) on \({P}\), whose pullback by the identity section under a gauge transformation satisfies

\(\displaystyle \check{\Theta}_{i}^{\prime}=\check{\gamma}_{i}\check{\Theta}_{i}\check{\gamma}_{i}^{-1}, \)

and which similarly across trivializing neighborhoods also undergoes a gauge transformation

\(\displaystyle \check{\Theta}_{i}=\check{g}_{ij}\check{\Theta}_{j}\check{g}_{ij}^{-1}. \)