One important way to construct spaces is using the procedure that defines a cell complex (AKA CW-complex):
Start with a discrete set of points, called 0-cells:
Attach line segments, called 1-cells, by their boundaries to form the 1-skeleton:

Attach disks, called 2-cells, by their boundaries to form the 2-skeleton:
We can then continue to any dimension by iteratively attaching n-cells, \({n}\)-dimensional disks \({D^{n}}\) in \({\mathbb{R}^{n}}\), by their boundaries, which are \({(n-1)}\)-dimensional spheres \({S^{n-1}}\), to form the n-skeleton.
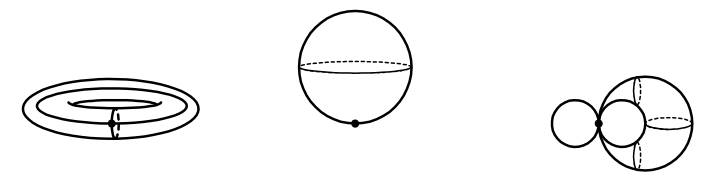
The first construction above illustrates that a torus with \({g}\) holes (genus \({g}\)) can be built from one 0-cell, 2\({g}\) 1-cells, and one 2-cell; the second illustrates that a sphere \({S^{n}}\) is one \({n}\)-cell attached to one 0-cell; and the third illustrates that the characteristic maps by which cells are attached can change the homotopy type of the resulting cell complex (in this case to an object which is not homotopy equivalent to the torus).
Can we always find a cell complex structure for the spaces we will be concerned with, mainly manifolds? Some facts are:
- Every compact manifold is homotopy equivalent to a cell complex
- Closed manifolds can always be given a cell complex structure, except in dimension 4 where the answer is unknown