Any element of the orthogonal group \({O\left(r,s\right)}\) is a rotation and/or reflection and the Cartan–Dieudonné theorem states that any such transformation can be obtained as a product of at most \({r+s}\) reflections. Thus every element of \({O\left(r,s\right)}\) corresponds to the Clifford product of some \({k}\) unit vectors via
\(\displaystyle R_{u_{k}\dotsm u_{1}}\left(v\right)\equiv R_{u_{k}}\left(\dotsm\left(R_{u_{1}}\left(v\right)\right)\dotsm\right)=\left(-1\right)^{k}u_{k}\dotsm u_{1}vu_{1}^{-1}\dotsm u_{k}^{-1}. \)
The elements of \({C\left(r,s\right)}\) that have the form of a Clifford product of unit vectors \({U=u_{k}\dotsm u_{1}}\) form a Lie group denoted \({\textrm{Pin}\left(r,s\right)}\) and called a Clifford group (AKA Pin group). In terms of the reverse operation of geometric algebra, the elements \({U\in\textrm{Pin}\left(r,s\right)}\) are products of invertible vectors which satisfy \({U\widetilde{U}=\pm1}\). \({R}\) forms a homomorphism from \({\textrm{Pin}\left(r,s\right)}\) to \({O\left(r,s\right)}\) defined by \({U\mapsto R_{U}}\), where
\(\displaystyle R_{U}(v)=\left(-1\right)^{k}UvU^{-1}. \)
This homomorphism is two-to-one, since \({R_{U}}\) and \({R_{-U}}\) map to the same transformation, so \({\textrm{Pin}(r,s)}\) is a double covering of \({O(r,s)}\).
Now, elements of \({SO\left(r,s\right)}\) are pure rotations, i.e. they are obtained as a product of an even number of reflections. Therefore the special Clifford group (AKA Spin group) \({\textrm{Spin}\left(r,s\right)\equiv\textrm{Pin}\left(r,s\right)\cap C_{0}\left(r,s\right)}\) is a double covering of \({SO\left(r,s\right)}\), using the restriction of \({R_{U}}\) to even elements:
\(\displaystyle R_{U}^{S}(v)=UvU^{-1} \)
| Δ It is important to remember that rotations in 4 dimensions and higher do not follow many intuitive ideas from 3 dimensions. In particular, a rotation can have more than one plane of rotation (where rotated vectors in the plane stay in the plane), and therefore can require more than two reflections. |
| Δ Distinctions are sometimes made between (special) Clifford groups and (S)Pin groups. |
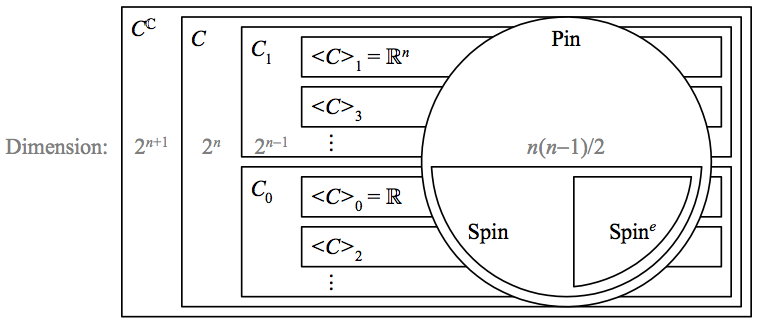
These relationships are depicted in the following diagram.
The above depicts how the Clifford group \({\textrm{Pin}}\) and its even subgroup \({\textrm{Spin}}\) are generated by the unit elements of the Clifford algebra \({C}\). \({C_{1}}\) and \({C_{0}}\) both have dimension \({2^{n-1}}\) as manifolds, and \({\textrm{Pin}}\), \({\textrm{Spin}}\), and \({\textrm{Spin}^{e}}\) all have dimension \({n(n-1)/2}\).
| Δ Some potential sources of confusion can be avoided by remembering that \({\textrm{Pin}\left(r,s\right)}\) is the group generated by Clifford multiplication on the unit elements of the algebra \({C\left(r,s\right)}\). Thus the elements of \({\textrm{Pin}\left(r,s\right)}\) can only be multiplied with each other and always have inverses, while the elements of \({C\left(r,s\right)}\) can be multiplied by scalars and added, but may not have multiplicative inverses. |