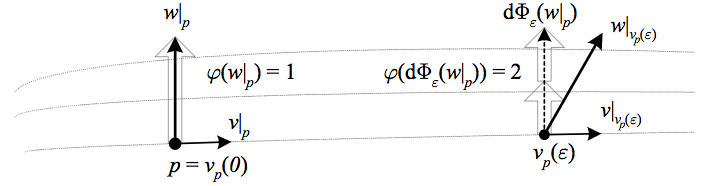The Lie derivative \({L_{v}}\) can be applied to a \({k}\)-form \({\varphi}\) by using the pullback of \({\varphi}\) by the diffeomorphism \({\Phi}\) associated with the flow of \({v}\), i.e. applied to \({k}\) vectors \({w_{I}}\) we define
\(\displaystyle L_{v}\varphi\left(w_{I}\right)\equiv\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left[\varphi\left(\mathrm{d}\Phi_{\varepsilon}\left(w_{I}\right)\right)-\varphi\left(w_{I}\right)\right]. \)
\({L_{v}\varphi}\) thus measures the change in \({\varphi}\) as its arguments are transported by the local flow of \({v}\). In the case of a 0-form \({f}\), this is just the differential or directional derivative \({L_{v}f=v(f)=\mathrm{d}f(v)}\).
The above illustrates the Lie derivative for a 1-form \({\varphi}\) with \({\varepsilon=1}\). \({L_{v}\varphi}\) is “the difference between \({\varphi}\) applied to \({w}\) and \({\varphi}\) applied to \({w}\) transported by the local flow of \({v}\),” so above we have \({L_{v}\varphi(w)=2-1=1}\) (valid in the limit \({\varepsilon\rightarrow0}\) if \({\varphi}\) changes linearly in the range shown).
By using the above definitions of the Lie derivative applied to vectors and 1-forms, and noting that we can derive a Leibniz rule over contraction \({L_{v}(\varphi\left(w\right))=\left(L_{v}\varphi\right)(w)+\varphi\left(L_{v}w\right)}\), we arrive at an expression for the Lie derivative applied to general tensors, viewed as real-valued mappings on vectors and 1-forms:
\begin{aligned}L_{v}T(\varphi_{1},\ldots,\varphi_{m},w_{1},\ldots,w_{n}) & =v\left(T(\varphi_{1},\ldots,\varphi_{m},w_{1},\ldots,w_{n})\right)\\
& -\sum_{j=1}^{m}T\left(\varphi_{1},\ldots,L_{v}\varphi_{j},\ldots,\varphi_{m},w_{1},\ldots,w_{n}\right)\\
& -\sum_{j=1}^{n}T\left(\varphi_{1},\ldots,\varphi_{m},w_{1},\ldots,L_{v}w_{j},\ldots,w_{n}\right)
\end{aligned}
In a holonomic frame, this yields an expression for the Lie derivative of a tensor in terms of coordinates
\begin{aligned}L_{v}T^{\mu_{1}\dots\mu_{m}}{}_{\sigma_{1}\dots\sigma_{n}} & =v^{\lambda}\frac{\partial}{\partial x^{\lambda}}T^{\mu_{1}\dots\mu_{m}}{}_{\sigma_{1}\dots\sigma_{n}}\\
& -\sum_{j=1}^{m}\left(\frac{\partial v^{\mu_{j}}}{\partial x^{\lambda}}\right)T^{\mu_{1}\dots\mu_{j-1}\lambda\mu_{j+1}\dots\mu_{m}}{}_{\sigma_{1}\dots\sigma_{n}}\\
& +\sum_{j=1}^{n}\left(\frac{\partial v^{\lambda}}{\partial x^{\sigma_{j}}}\right)T^{\mu_{1}\dots\mu_{m}}{}_{\sigma_{1}\dots\sigma_{j-1}\lambda\sigma_{j+1}\dots\sigma_{n}}.
\end{aligned}
From this we can confirm that the Lie derivative satisfies the Leibniz rule over the tensor product, and therefore is a derivation of degree 0 on both the tensor algebra and the exterior algebra.