Compact Lie groups have many properties that make them an easier class to work with in general, including:
- Every compact Lie group has a faithful representation (and so can be viewed as a matrix group with real or complex entries)
- Every representation of a compact Lie group is similar to a unitary representation (and so is similar to a subgroup of \({U(n)}\) for some \({n}\))
- The Haar measure is bi-invariant on a compact Lie group
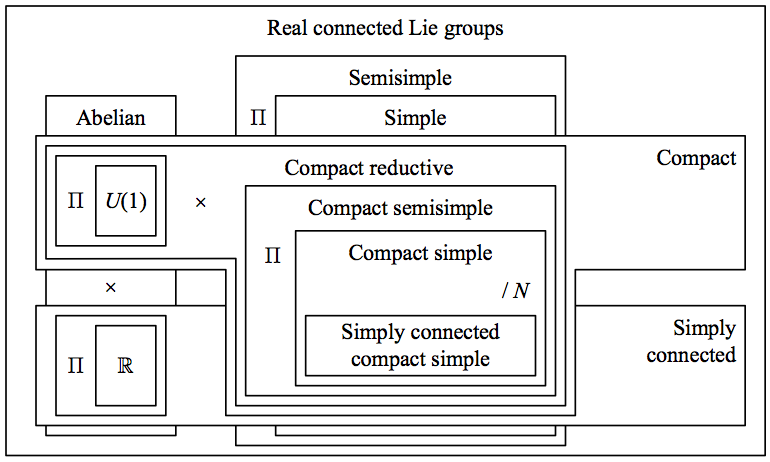
In terms of classification, it turns out that any compact Lie group has a Lie algebra that can be expressed as a direct sum of certain classes of Lie algebras. Recall that an abelian Lie algebra is one whose Lie bracket is identically zero. As one would expect, an abelian Lie group, one with an abelian Lie algebra, is also abelian in the group sense. A simple Lie algebra is a non-abelian one that has no nonzero proper ideal, and a simple Lie group is one with a simple Lie algebra. Sometimes a simple Lie group is defined to be one that is simple in a group sense. Note that this is a distinct definition, since in general a simple Lie group \({G}\) in our sense is not simple in the group sense: it may have discrete normal subgroups corresponding to other Lie groups covered by \({G}\).
A Lie algebra that is a direct sum of simple Lie algebras is called a semisimple Lie algebra, and a semisimple Lie group is one with a semisimple Lie algebra. For any element \({A}\) in a semisimple Lie algebra, there are elements \({B}\) and \({C}\) with \({A=\left[B,C\right]}\); thus it is a rough “opposite” to an abelian Lie algebra. Finally, a Lie algebra that is the direct sum of simple Lie algebras and abelian ones is called a reductive Lie algebra, and a reductive Lie group is one with a reductive Lie algebra (however, other definitions of reductive Lie group are sometimes used).
For our purposes, the important fact is this: any compact connected Lie group is a reductive group. Since every abelian connected compact Lie group is a direct product of copies of \({U(1)}\), and since every simple compact connected Lie group is a quotient of its universal covering group by a discrete normal subgroup, we can thus reduce the classification of compact connected Lie groups to that of simply connected compact simple Lie groups. This rather overwhelming scheme may possibly be clarified if viewed pictorially.
The above depicts the fact that any compact connected Lie group is of the form \({G/N}\), where \({G}\) is a direct product of copies of \({U(1)}\) and simply connected compact simple Lie groups, and \({N}\) is a normal discrete subgroup of \({G}\).