A vector field \({w}\) on \({M}\) can be viewed as a vector-valued 0-form. As noted previously, the covariant derivative \({\nabla_{v}w}\) is linear in \({v}\) and depends only on its local value, and so can be viewed as a vector-valued 1-form \({\mathrm{D}\vec{w}(v)\equiv\nabla_{v}w}\). \({\mathrm{D}\vec{w}}\) is called the exterior covariant derivative of the vector-valued 0-form \({\vec{w}}\). This definition is then extended to vector-valued \({k}\)-forms \({\vec{\varphi}}\) by following the example of the exterior derivative \({\mathrm{d}}\):
\begin{aligned} & \mathrm{D}\vec{\varphi}\left(v_{0},\dotsc,v_{k}\right)\\ & \equiv\underset{j=0}{\overset{k}{\sum}}\left(-1\right)^{j}\nabla_{v_{j}}\left(\vec{\varphi}\left(v_{0},\dotsc,v_{j-1},v_{j+1},\dotsc,v_{k}\right)\right)\\ & \phantom{{}=}+\underset{i<j}{\sum}\left(-1\right)^{i+j}\vec{\varphi}\left(\left[v_{i},v_{j}\right],v_{0},\dotsc,v_{i-1},v_{i+1},\dotsc,v_{j-1},v_{j+1},\dotsc,v_{k}\right) \end{aligned}
For example, if \({\vec{\varphi}}\) is a vector-valued 1-form, we have
\(\displaystyle \mathrm{D}\vec{\varphi}\left(v,w\right)\equiv\nabla_{v}\vec{\varphi}\left(w\right)-\nabla_{w}\vec{\varphi}\left(v\right)-\vec{\varphi}\left(\left[v,w\right]\right). \)
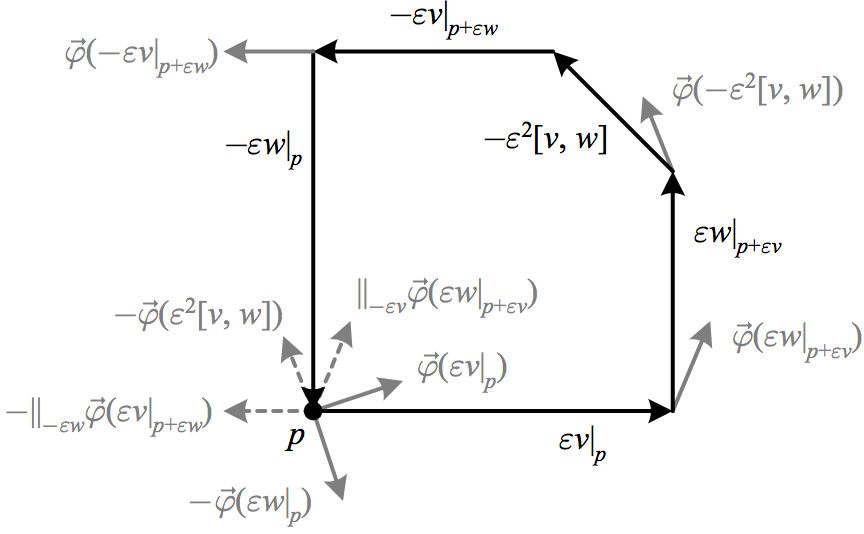
So while the first term of \({\mathrm{d}\varphi}\) takes the difference between the scalar values of \({\varphi(w)}\) along \({v}\), the first term of \({\mathrm{D}\vec{\varphi}}\) takes the difference between the vector values of \({\vec{\varphi}(w)}\) along \({v}\) after parallel transporting them to the same point (which is required to compare them). At a point \({p}\), \({\mathrm{D}\vec{\varphi}\left(v,w\right)}\) can thus be viewed as the “sum of \({\vec{\varphi}}\) on the boundary of the surface defined by its arguments after being parallel transported back to \({p}\),” and if we use \({\Vert_{\varepsilon v}}\) to denote parallel transport along an infinitesimal curve with tangent \({v}\), we can write
\begin{aligned}\varepsilon^{2}\mathrm{D}\vec{\varphi}\left(v,w\right) & =\Vert_{-\varepsilon v}\vec{\varphi}\left(\varepsilon w\left|_{p+\varepsilon v}\right.\right)-\vec{\varphi}\left(\varepsilon w\left|_{p}\right.\right)\\ & -\Vert_{-\varepsilon w}\vec{\varphi}\left(\varepsilon v\left|_{p+\varepsilon w}\right.\right)+\vec{\varphi}\left(\varepsilon v\left|_{p}\right.\right)\\ & -\vec{\varphi}\left(\varepsilon^{2}\left[v,w\right]\right).\end{aligned}
The above depicts how the exterior covariant derivative \({\mathrm{D}\vec{\varphi}\left(v,w\right)}\) sums the vectors \({\vec{\varphi}}\) along the boundary of the surface defined by \({v}\) and \({w}\) by parallel transporting them to the same point. Note that the “completion of the parallelogram” \({[v,w]}\) is already of order \({\varepsilon^{2}}\), so its parallel transport has no effect to this order.
From its definition, it is clear that \({\mathrm{D}\vec{\varphi}}\) is a frame-independent quantity. In terms of the connection, we must consider \({\vec{w}}\) as a frame-dependent \({\mathbb{R}^{n}}\)-valued 0-form, so that
\(\displaystyle \mathrm{D}\vec{w}\left(v\right)=\nabla_{v}w=\mathrm{d}\vec{w}\left(v\right)+\check{\Gamma}\left(v\right)\vec{w}. \)
For a \({\mathbb{R}^{n}}\)-valued \({k}\)-form \({\vec{\varphi}}\) we find that
\(\displaystyle \mathrm{D}\vec{\varphi}=\mathrm{d}\vec{\varphi}+\check{\Gamma}\wedge\vec{\varphi}, \)
where the exterior derivative is defined to apply to the frame-dependent components, i.e. \({\mathrm{d}\vec{\varphi}(v_{0}\ldots v_{k})\equiv\mathrm{d}\varphi^{\mu}(v_{0}\ldots v_{k})e_{\mu}}\). Recall that \({\check{\Gamma}}\) is a \({gl(n,\mathbb{R})}\)-valued 1-form, so that for example if \({\vec{\varphi}}\) is a \({\mathbb{R}^{n}}\)-valued 1-form then \({(\check{\Gamma}\wedge\vec{\varphi})\left(v,w\right)\equiv\check{\Gamma}\left(v\right)\vec{\varphi}\left(w\right)-\check{\Gamma}\left(w\right)\vec{\varphi}\left(v\right)=\Gamma^{\lambda}{}_{\mu}\left(v\right)\varphi^{\mu}\left(w\right)-\Gamma^{\lambda}{}_{\mu}\left(w\right)\varphi^{\mu}\left(v\right)}\).
| Δ As with the covariant derivative, it is important to remember that \({\mathrm{D}\vec{\varphi}}\) is frame-independent while \({\mathrm{d}\vec{\varphi}}\) and \({\check{\Gamma}}\) are not. |
The set of vector-valued forms can be viewed as an infinite-dimensional algebra by defining multiplication via the vector field commutator; it turns out that \({\mathrm{D}}\) does not satisfy the Leibniz rule in this algebra and so is not a derivation. However, following the above reasoning one can extend the definition of \({\mathrm{D}}\) to the algebra of tensor-valued forms, or the subset of anti-symmetric tensor-valued forms; \({\mathrm{D}}\) then is a derivation with respect to the tensor product in the former case and a graded derivation with respect to the exterior product in the latter case. We will not pursue either of these two generalizations.