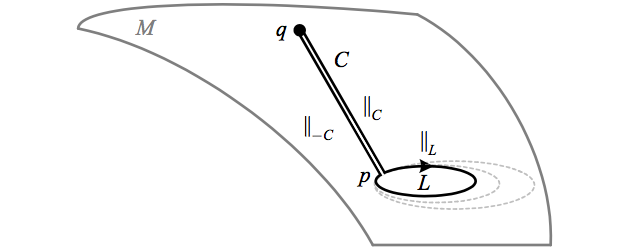
We have seen that on a manifold with connection, the curvature measures the effect of a vector being parallel transported around an infinitesimal loop. If we consider the set of all closed loops at a basepoint \({p}\) on a connected manifold with connection \({M^{n}}\), the associated linear transformations due to parallel transport of a vector around each loop form a group called the holonomy group \({\mathrm{Hol}(M)}\). The restricted holonomy group \({\mathrm{Hol}^{0}(M)}\) only counts loops homotopic to zero.
From the definition of the parallel transporter we can see that \({\mathrm{Hol}(M)}\) is in fact a group, and also a subgroup of \({GL(\mathbb{R}^{n})}\), and therefore a Lie group. We can also see that for a connected manifold it is independent of the basepoint \({p}\), since changing basepoints induces a similarity transformation (change of basis), altering the matrix representation of the group but acting as an isomorphism on the abstract group. If \({M}\) is simply connected, then \({\mathrm{Hol}^{0}(M)=\mathrm{Hol}(M)}\); if not, then \({\mathrm{Hol}^{0}(M)}\) is the identity component of \({\mathrm{Hol}(M)}\), which is a group representation of the fundamental group of \({M}\) called the monodromy representation.
The above depicts how the holonomy group is comprised of elements \({\parallel_{L}\in GL(\mathbb{R}^{n})}\) associated with parallel transport around loops; changing the basepoint of the loop from \({p}\) to \({q}\) induces a similarity transformation \({\parallel_{C}^{-1}\parallel_{L}\parallel_{C}}\), leaving the abstract group unchanged.
Since the curvature is the infinitesimal version of the holonomy construction, we might expect that it be related to the Lie algebra of \({\mathrm{Hol}(M)}\), which is called the holonomy algebra. The Ambrose-Singer theorem confirms this; in the case of a simply connected manifold, it says that the Lie algebra of \({\mathrm{Hol}(M)}\) is generated by all elements of the form \({\check{R}(v,w)\left|_{q\in M}\right.}\).
Zero holonomy group then implies zero curvature; but the converse is only true for the restricted holonomy group, as can be seen by considering e.g. a flat sheet of paper rolled into a cone. However, zero curvature implies that the holonomy algebra vanishes, which means that the holonomy group is discrete.