Generalizing the fundamental group to higher dimensions yields the homotopy groups \({\pi_{n}(X)}\), which count how many ways \({S^{n}}\) can be mapped into a path-connected space \({X}\).

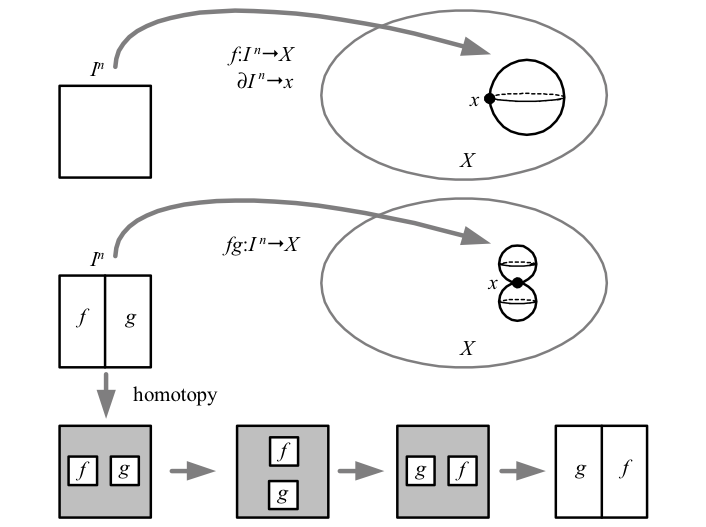
Group multiplication is similarly implemented by dividing the \({n}\)-cube \({I^{n}}\) in half along one dimension, and applying the maps to be multiplied to each half. Just as we required homotopies of loops to map endpoints to the basepoint, we here require the boundary of \({I^{n}}\) to map to the basepoint. Unlike \({\pi_{1}}\), \({\pi_{n}}\) is abelian for \({n>1}\). This is because there is no “room” in one dimension to homotopically swap the spheres as there is in two or more dimensions.

Above we see that in more than one dimension, maps from the two halves of \({I^{n}}\) can be homotopically swapped, making \({\pi_{n}}\) abelian. The shaded surfaces in the figure are mapped to the basepoint \({x}\) along with the boundaries.

Although the homotopy groups as a measuring tool share the incompleteness that characterizes all of algebraic topology, i.e. equal \({\pi_{n}}\) do not guarantee homotopy equivalent spaces, there is a theorem that comes close. Whitehead’s theorem states that a map between cell complexes that induces isomorphisms on all \({\pi_{n}}\) is a homotopy.