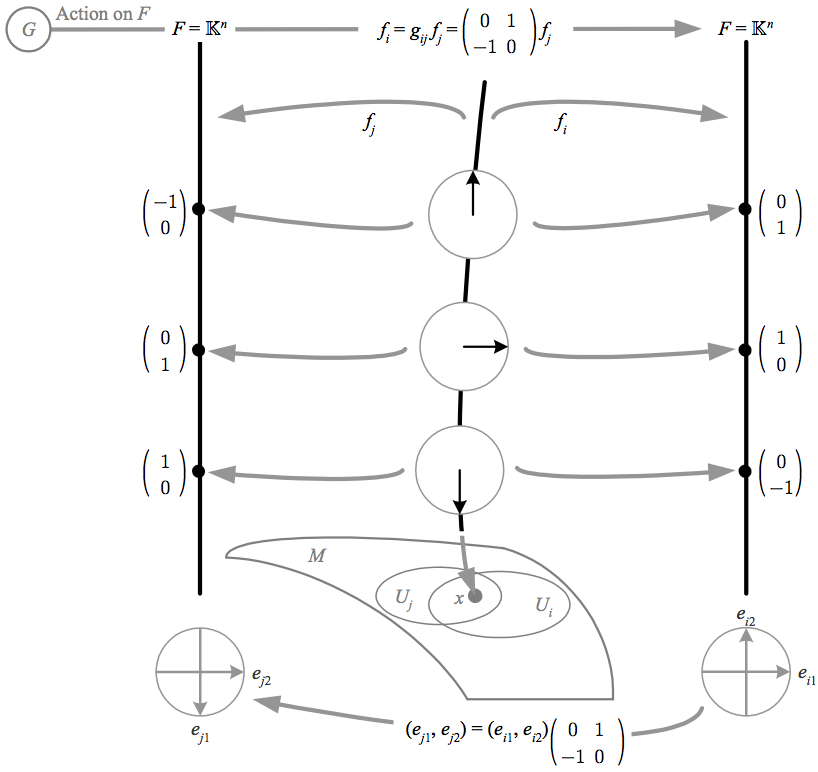
A vector bundle \({(E,M,\pi,\mathbb{K}^{n})}\) has a vector space fiber \({\mathbb{K}^{n}}\) (assumed here to be \({\mathbb{R}^{n}}\) or \({\mathbb{C}^{n}}\)) and a structure group that is linear (\({G\subseteq GL(n,\mathbb{K})}\)) and therefore acts as a matrix across trivializing neighborhoods, i.e.

\(\displaystyle f_{i}(p)=g_{ij}f_{j}(p), \)

where the operation of \({g_{ij}}\) is now matrix multiplication on the vector components \({f_{j}(p)\in\mathbb{K}^{n}}\). If we view \({V_{x}\equiv\pi^{-1}(x)}\) as an internal space on \({M}\) with intrinsic vector elements \({v}\), the linear map \({f_{i}\colon\pi^{-1}(x)\rightarrow\mathbb{K}^{n}}\) is equivalent to choosing a basis \({e_{i\mu}}\) to get vector components, i.e. \({f_{i}(v)=v_{i}^{\mu}}\), where \({v_{i}^{\mu}e_{i\mu}=v}\) (and latin letters are labels while greek letters are the usual indices for vectors and labels for bases). The action of the structure group can then be written

\(\displaystyle v_{i}^{\mu}=(g_{ij})^{\mu}{}_{\lambda}v_{j}^{\lambda}, \)

which is equivalent to a change of basis

\(\displaystyle e_{i\mu}=(g_{ij}^{-1})^{\lambda}{}_{\mu}e_{j\lambda}, \)

or as matrix multiplication on basis row vectors

\(\displaystyle e_{j}=e_{i}g_{ij}, \)

so that the action of \({g_{ij}(x)}\) in \({U_{i}\cap U_{j}}\) is equivalent to a change of frame or gauge transformation from \({e_{i}}\) to \({e_{j}}\), which is equivalent to a transformation of internal space vector components in the opposite direction.

If the structure group of a vector bundle is reducible to \({GL(n,\mathbb{K})^{e}}\), then it is called an orientable bundle; all complex vector bundles are orientable, so orientability usually refers to real vector bundles. The tangent bundle of \({M}\) (formally defined in an upcoming section) is then orientable iff \({M}\) is orientable. On a pseudo-Riemannian manifold \({M}\), the structure group of the tangent bundle is reducible to \({O(r,s)}\), and if \({M}\) is orientable then it is reducible to \({SO(r,s)}\); if the structure group can be further reduced to \({SO(r,s)^{e}}\), then \({M}\) and its tangent bundle are called time and space orientable. Note that this additional distinction is dependent only upon the metric, and two metrics on the same manifold can have different time and space orientabilities.

A gauge transformation on a vector bundle is a smoothly defined linear transformation of the basis inferred by the components due to local trivializations at each point, i.e.

\(\displaystyle e_{i\mu}^{\prime}=(\gamma_{i}^{-1})^{\lambda}{}_{\mu}e_{i\lambda}, \)

which is equivalent to new local trivializations where

\(\displaystyle \left(v_{i}^{\mu}\right)^{\prime}=(\gamma_{i})^{\mu}{}_{\lambda}v_{i}^{\lambda}, \)

giving us new transition functions

\(\displaystyle g_{ij}^{\prime}=\gamma_{i}g_{ij}\gamma_{j}^{-1}, \)

where we have suppressed indices for pure matrix relationships. Thus the gauge group is the same as the structure group, and a gauge transformation \({\gamma_{i}^{-1}}\) is equivalent to the transition function \({g_{i^{\prime}i}}\) from \({U_{i}}\) to \({U_{i}^{\prime}}\), the same neighborhood with a different local trivialization.

The above depicts how the elements of the fiber over \({x}\) in a vector bundle can be viewed as abstract vectors in an internal space, with the local trivialization acting as a choice of basis from which the components of these vectors can be calculated. The structure group then acts as a matrix transformation between vector components, and between bases in the opposite direction. A gauge transformation is also a new choice of basis, and so can be handled similarly.

A vector bundle always has global sections (e.g. the zero vector in the fiber over each point). A vector bundle with fiber \({\mathbb{R}}\) is called a line bundle.