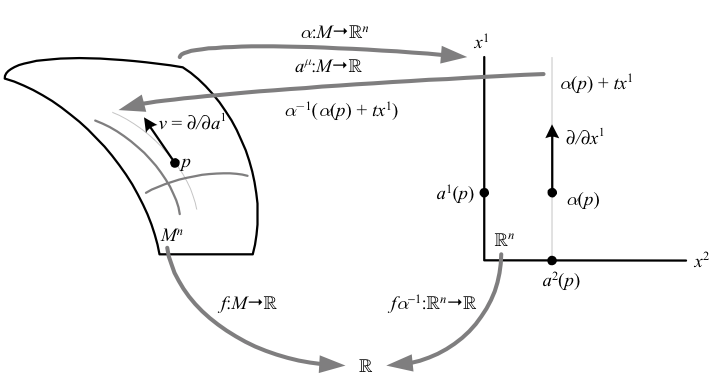
The tangent space \({T_{p}U}\) at a point \({p\in U}\) is defined to be the vector space spanned by the differential operators \({\partial/\partial a^{\mu}\mid_{p}}\). A tangent vector \({v\in T_{p}U}\) can then be expressed in tensor component notation as \({v=v^{\mu}\partial/\partial a^{\mu}}\), so that \({v\left(a^{\mu}\right)=v^{\mu}}\). The tangent vector \({\partial/\partial a^{\mu}\mid_{p}}\) applied to a function \({f}\) can be thought of as “the change of \({f}\) in the direction of the \({\mu^{\textrm{th}}}\) coordinate line at \({p}\).”
Thus at a point \({p}\), we have
\(\displaystyle v^{\mu}\frac{\partial}{\partial a^{\mu}}\left(f\right)=v^{\mu}\frac{\partial}{\partial x^{\mu}}\left(f\circ\alpha^{-1}\left(x\right)\right), \)
where \({x=\alpha(p)}\). The coordinate line \({\alpha^{-1}\left(a^{\mu}\left(p\right)+tv^{\mu}x^{\mu}\right)}\) is a parameterized curve on \({M}\), and thus it and the tangent vector itself are coordinate-independent objects. In this chart, any parametrized curve is defined to have tangent \({v}\) at \({t=0}\) if its coordinates are \({C^{\mu}\left(t\right)\equiv a^{\mu}+tv^{\mu}}\) to first order in \({t}\); therefore the coordinates of the tangent vector to \({C}\) at any point may be obtained by
\(\displaystyle v^{\mu}=\frac{\mathrm{d}C^{\mu}}{\mathrm{d}t}. \)
In another coordinate chart, the coordinate line that yields the same operator on functions near \({p}\) can be seen to correspond to the familiar transformation of vector components
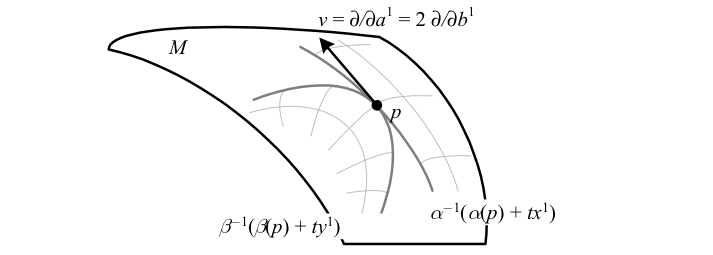
\(\displaystyle v=v^{\mu}\frac{\partial}{\partial a^{\mu}}=\left(v^{\lambda}\frac{\partial b^{\mu}}{\partial a^{\lambda}}\right)\frac{\partial}{\partial b^{\mu}}. \)
We can consider the point “\({p}\) moved in the direction \({v}\)” by abusing notation to write \({p^{\mu}+tv^{\mu}}\) in place of \({\alpha^{-1}\left(a^{\mu}\left(p\right)+tv^{\mu}x^{\mu}\right)}\); this is a coordinate-dependent expression, but in the limit \({\varepsilon\rightarrow0}\) we can unambiguously write \({p+\varepsilon v}\) to refer to the concept “\({p}\) moved infinitesimally in the direction \({v}\),” which is coordinate-independent. This allows us to write
\(\displaystyle v(f)=\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left[f_{p+\varepsilon v}-f_{p}\right]. \)
The above depicts a tangent vector \({v}\) in terms of two different coordinate charts. \({v^{\mu}=(1,0)}\) in chart \({\alpha}\) with coordinate functions \({a^{\mu}\left(p\right)=x^{\mu}}\), and \({v^{\mu}=\left(2,0\right)}\) in chart \({\beta}\) with coordinate functions \({b^{\mu}\left(p\right)=y^{\mu}}\). The divergent coordinate lines show that the concept of moving a point “in the direction of \({v}\)” can only be coordinate-independent in the infinitesimal limit.
The set of all tangent spaces in a region \({U}\) is called the tangent bundle, and is denoted \({TU}\). A (smooth, contravariant) vector field on \({U}\) is then a tangent vector defined at each point such that its application to a smooth function on \({U}\) is again smooth. Similarly, covariant vector field is a \({1}\)-form defined in the cotangent space \({T_{p}^{*}U}\) at each point such that its value on a vector field is a smooth function, and the set of all cotangent spaces \({T^{*}U}\) is called the cotangent bundle. A tensor field is then the tensor product of vector fields and covariant vector fields.
| Δ Tensor fields (including vector fields and covariant vector fields) are written using the same notation as tensors, making it important to distinguish the two situations. In particular, one can define a (pseudo) metric tensor field, which is then usually referred to as simply a metric. |
Note that a tensor field must remain a tensor locally at any point \({p}\), i.e. it must be a multi-linear mapping. For example, a covariant tensor field can only depend upon the values of its vector field arguments at \({p}\), since otherwise one could add a vector field that vanishes at \({p}\) and obtain a different result. This means that operators such as the derivatives on manifolds we will see here and here cannot usually be viewed as tensors, since they measure the difference between arguments at different points.
Since vectors are operators on functions, we can apply one vector field to another. Following the practice of using \({\partial/\partial x^{u}}\) to refer to \({\partial/\partial a^{\mu}}\), this can be used to define the Lie bracket of vector fields
\begin{aligned}\left[v,w\right](f) & \equiv v(w(f))-w(v(f))\\
\Rightarrow\left[v,w\right] & =\left(v^{\mu}\frac{\partial w^{\lambda}}{\partial x^{\mu}}-w^{\mu}\frac{\partial v^{\lambda}}{\partial x^{\mu}}\right)\frac{\partial}{\partial x^{\lambda}}.
\end{aligned}
Here we have used the equality of mixed partials, and can easily verify that \({\left[v,w\right]}\) is anti-commuting and satisfies the Jacobi identity. Since this expression is coordinate-independent, \({\left[v,w\right]}\) is a vector field and we can thus view \({\textrm{vect}\left(M\right)}\), the set of all vector fields on \({M}\), as the infinite-dimensional Lie algebra of vector fields on \({M}\), with vector multiplication defined by the Lie bracket.
Having defined vector and tensor fields on manifolds, we can now define a differential form as an alternating covariant tensor field, i.e. an exterior form in \({\Lambda\left(T_{p}U\right)}\) smoothly defined for every point \({p}\).
| Δ Just as tensor fields are usually referred to as simply tensors, differential forms are usually referred to as simply forms, and a \({k}\)-form is written simply \({\varphi\in\Lambda^{k}M}\). It is important to remember that in the context of manifolds, a \({k}\)-form is an exterior form smoothly defined on \({k}\) elements of the tangent space at each point, i.e. an anti-symmetric covariant \({k}\)-tensor field. |
On a differentiable manifold, the existence of \({k}\)-forms makes possible a more concrete definition of orientability: a manifold \({M^{n}}\) is orientable iff there exists a non-vanishing \({n}\)-form. Such a form is called a volume form (AKA volume element), since as we recall it gains a Jacobian-like determinant factor under invertible linear transformations.
| Δ The term “volume form” or “volume element” is sometimes defined in physics to reflect the intuitive idea of a form which returns the volume spanned by its argument vectors; however, volume is always positive, so that in this usage we are more accurately referring to a volume pseudo-form whose value is the absolute value of the volume form as we have defined it, and which exists on any differentiable manifold, including those which are non-orientable. |