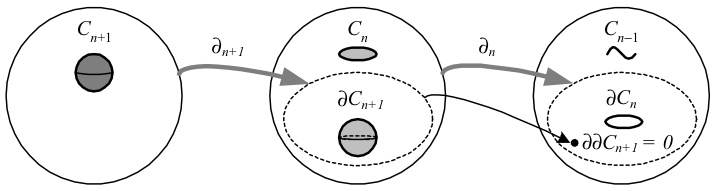
A fundamental intuitive fact reproduced in this formalism is that the boundary of a boundary is zero. A useful algebraic generalization of this idea is the chain complex, defined to be a sequence of homomorphisms of abelian groups \({\partial_{n}\colon C_{n}\to C_{n-1}}\) with \({\partial_{n}\partial_{n+1}=0}\). In our case the abelian groups \({C_{n}}\) are the \({n}\)-chains, and the chain complex can be illustrated as follows:
Note that the image of \({\partial_{n+1}}\) is contained in the kernel of \({\partial_{n}}\); if these are in fact equal, the chain complex is an exact sequence, defined to be any sequence of homomorphisms for which the image of one object is the kernel of the next. A short exact sequence is of the form
\(\displaystyle 0\longrightarrow N\overset{\phi}{\longrightarrow}E\overset{\pi}{\longrightarrow}G\longrightarrow0,\)
and any longer sequence is called a long exact sequence. \({\phi}\) is injective and \({\pi}\) is surjective, so a short exact sequence can be viewed as an embedding of \({N}\) into \({E}\) with \({G=E/N}\). For groups, a short exact sequence is called a group extension, or “\({E}\) is an extension of \({G}\) by \({N}\).” Note that \({N}\) is normal in \({E}\) since it is the kernel of \({\pi}\), and thus \({G\cong E/N}\). A central extension is one where \({N}\) also lies in the center of \({E}\).
| Δ A group extension as above is sometimes described as “\({E}\) is an extension of \({N}\) by \({G}\).” A long exact sequence is sometimes defined as any exact sequence that is not short, or as one which is infinite. |