A matter field can also transform as a spinor, in which case it is called a spinor matter field (AKA spinor field), and is a 0-form on \({M}\) which e.g. for Dirac spinors takes values in \({V\otimes\mathbb{C}^{4}}\). The gauge component then responds to gauge transformations, while the spinor component responds to changes of frame. Similarly, a matter field on \({M^{r+s}}\) taking values in \({V\otimes\mathbb{R}^{r+s}}\) is called a vector matter field (AKA vector field), where the vector component responds to changes of frame. Finally, a matter field without any frame-dependent component is called a scalar matter field (AKA scalar field), and a matter field taking values in \({\mathbb{C}}\) (which can be viewed as either vectors or scalars) is called a complex scalar matter field (AKA complex scalar field, scalar field). A spinor matter field with gauge group \({U(1)}\) is called a charged spinor field.
| Δ It is important remember that spinor and vector matter fields use the tensor product, not the direct sum, and therefore cannot be treated as two independent fields. In particular, the field value \({\phi\otimes\psi\in V\otimes\mathbb{C}^{4}}\) is identical to the value \({-\phi\otimes-\psi}\), which has consequences regarding the existence of global spinor fields, as we will see in the section on spinor bundles. |
In order to directly map changes of frame to spinor field transformations, one must use an orthonormal frame so all changes of frame are rotations. The connection associated with an orthonormal frame is therefore called a spin connection, and takes values in \({so(3,1)\cong\mathrm{spin}(3,1)}\). Thus the spin connection and gauge potential together provide the overall transformation of a spinor field under parallel transport. All of the above can be generalized to arbitrary dimension and signature.
| Tangent space \({T_{p}M\cong\mathbb{R}^{(r+s)}}\) | Spinor space \({S_{p}\cong\mathbb{K}^{m}}\) | Internal space \({V_{p}\cong\mathbb{C}^{n}}\) |
|---|---|---|
| Frame | Standard basis of \({\mathbb{K}^{m}}\) identified with an initial orthonormal frame on \({M}\) | Gauge |
| Change of frame | \({U_{p}\in\mathrm{Spin}(r,s)}\) associated with change of orthonormal frame \({\check{\gamma}_{p}}\) | Gauge transformation |
| Vector field \({p\mapsto w\in T_{p}M}\) | Spinor field \({p\mapsto\psi\in S_{p}}\) | Complex / YM field \({p\mapsto\phi\in V_{p}}\) |
| Connection \({v\mapsto\check{\Gamma}\left(v\right)\in gl(r,s)}\) | Spin connection \({v\mapsto\check{\omega}\left(v\right)\in so(r,s)}\), the bivectors | Gauge potential \({v\mapsto\check{A}\left(v\right)\in gl(n,\mathbb{C})}\) |
| Curvature \({\check{R}=\mathrm{d}\check{\Gamma}+\check{\Gamma}\wedge\check{\Gamma}}\) | Curvature \({\check{R}=\mathrm{d}\check{\omega}+\check{\omega}\wedge\check{\omega}}\) | Field strength \({\check{F}=\mathrm{d}\check{A}-iq\check{A}\wedge\check{A}}\) |
Constructs as applied to the various spaces associated with a point \({p\in M}\) in spacetime and a vector \({v}\) at \({p}\).
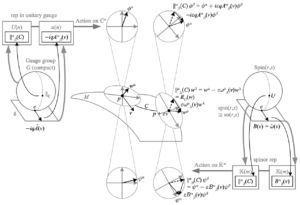
The above depicts how a matter field can be the tensor product of a complex scalar or Yang-Mills field \({\phi}\) and a spinor field \({\psi}\). YM fields use a connection and gauge (frame) which are independent of the spacetime manifold frame, while spinor fields mirror the connection and changes in frame of the spacetime manifold. YM fields are acted on by reps of the gauge group and its Lie algebra, while spinor fields are acted on by reps of the Spin group and its Lie algebra. In the figure we assume an infinitesimal curve \({C}\) with tangent \({v}\), an orthonormal frame, a spin connection, and a unitary gauge. Note that the field components shown at \({p+\varepsilon v}\) are those of the field value at \({p}\) applied to the frame at \({p+\varepsilon v}\), i.e. the top right field vector depicted would be more precisely written \({\left.\phi^{\alpha}\right|_{p}\left.e_{\alpha}\right|_{p+\varepsilon v}}\); in particular, this quantity is unrelated to the value of the field \({\left.\phi^{\alpha}\right|_{p+\varepsilon v}}\).
| Δ Note that a Lorentz transformation on all of flat Minkowski space, which is the setting for many treatments of this material, induces a change of coordinate frame that is the same Lorentz transformation on every tangent space, thus simplifying the above picture by eliminating the need to consider parallel transport on the curved spacetime manifold. |
| Δ The spinor space is an internal space, but its changes of frame are driven by those of the spacetime manifold. The question of whether a global change of orthonormal frame can be mapped to globally defined elements in \({\mathrm{Spin}(r,s)}\) across coordinate charts in a consistent way is resolved later in terms of fiber bundles. |