The relationship between Lie groups and Lie algebras is particularly straightforward for simply connected Lie groups:
- Every Lie algebra corresponds to a unique simply connected Lie group \({G^{*}}\)
- There is a group homomorphism \({\phi}\) from this unique simply connected Lie group \({G^{*}}\) to any other connected Lie group \({G}\) with the same Lie algebra, with \({\textrm{Ker}\phi\cong\pi_{1}\left(G\right)}\) discrete
This last implies that for any Lie group \({G\cong G^{*}/\pi_{1}\left(G\right)}\), the simply connected Lie group \({G^{*}}\) with the same Lie algebra has a fixed number of points that map down to any point in \({G}\). \({G^{*}}\) can thus be pictured as “wrapping around” any such \({G}\) some number of times, and is therefore called the universal covering group.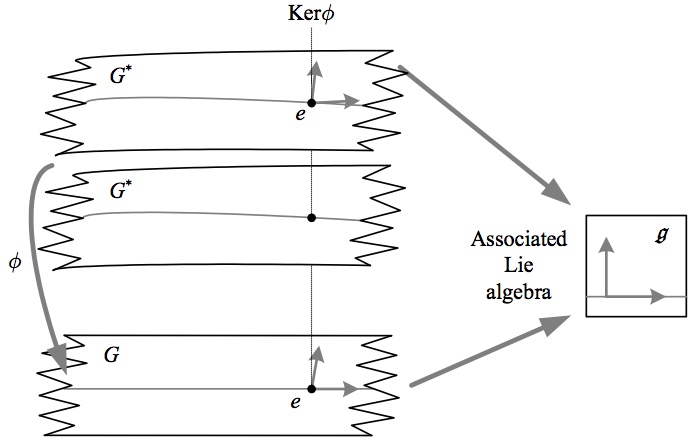
The above depicts the universal covering group \({G^{*}}\) and its homomorphism to any other Lie group \({G}\) with the same Lie algebra. A one-dimensional subalgebra and corresponding one-dimensional subgroups are shown as lines.
The idea of a space covering another generalizes to any topological space: a covering space \({C}\) of a space \({X}\) has a continuous surjective map to \({X}\) whose inverse in a neighborhood of any point of \({X}\) is a union of mutually disjoint open sets homeomorphic to that neighborhood. The points that map to a point \({p\in X}\) are called the fiber over \({p}\), and the disjoint open sets over a neighborhood of \({p}\) are called sheets. Under reasonable connectivity requirements, every space then has a unique simply connected universal covering space that covers all connected covers.
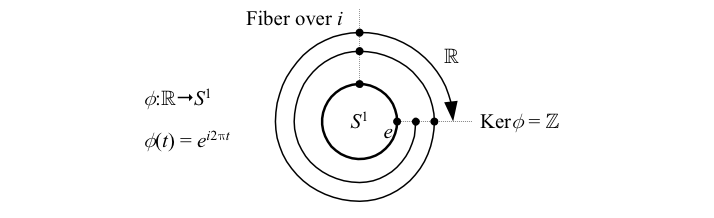
The above depicts the infinite-sheeted universal covering space \({\mathbb{R}}\) of \({S^{1}}\).