For a closed orientable topological manifold \({M^{n}}\), Poincaré duality refers to a symmetry that relates the \({k^{\textrm{th}}}\) homology group to the \({\left(n-k\right)^{\textrm{th}}}\) group. This symmetry has several consequences:
- There are canonical isomorphisms \({H_{k}\cong H^{n-k}}\) for all \({k}\)
- \({H_{k}\cong H_{n-k}}\) modulo their torsion subgroups, i.e. modulo the \({\mathbb{Z}}\) summands with torsion coefficients \({\Leftrightarrow}\) in terms of Betti numbers, \({b_{k}=b_{n-k}}\)
- The torsion subgroups of \({H_{k}}\) and \({H_{n-k-1}}\) are isomorphic
- For a closed non-orientable \({M,H_{k}\left(M;\mathbb{Z}_{2}\right)\cong H^{n-k}\left(M;\mathbb{Z}_{2}\right)}\)
For orientable non-compact manifolds, a more complicated duality map can also be constructed.
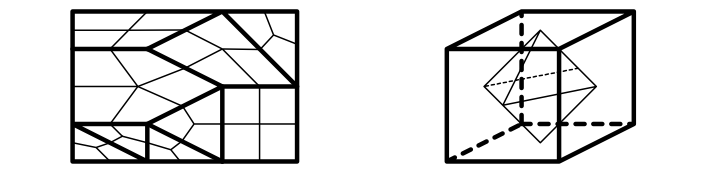
Geometrically, Poincaré duality expresses the existence of dual cell structures on a manifold. For example, in two dimensions the dual is obtained from any cell structure by placing a vertex at the center of every face, with an edge bisecting every original edge. Triangulating the sphere in this way with a regular cell structure yields a polyhedron, and one obtains the dual polyhedron by placing a vertex at the center of each face.
The Platonic solids, i.e. the five convex polyhedra with identical convex regular polygonal faces, are all dual to one another, as the cube is dual to the octahedron above. This dual cell structure concept can be generalized to arbitrary dimension, and this can be seen to lead directly to the symmetry between homology on the original cell structure and cohomology on the dual cell structure.
Alexander duality relates homology and cohomology groups for a sphere with a piece deleted: for \({U}\) a compact locally contractible subspace of \({S^{n}}\), \({H_{k}\left(S^{n}-U;\mathbb{Z}\right)\cong H^{n-k-1}\left(U;\mathbb{Z}\right)}\).