With the matrix isomorphisms of the previous section in hand, the representation theory of Clifford algebras is quite simple, although the terminology is less so due to historical artifacts. First we note that for \({\mathbb{K}\equiv\mathbb{R}}\), \({\mathbb{C}}\), or \({\mathbb{H}}\), \({\mathbb{K}(n)\cong\mathbb{K}\otimes\mathbb{R}(n)}\), and as we will see in the section on Pauli matrices, \({\mathbb{C}}\) is isomorphic to a subalgebra of \({\mathbb{R}(2)}\) and \({\mathbb{H}}\) is isomorphic to a subalgebra of \({\mathbb{R}(4)}.\) This gives a representation of \({\mathbb{C}(n)}\) on \({\mathbb{R}^{2n}}\), which is in fact its only real faithful irreducible rep, and similarly gives \({\mathbb{H}(n)}\) a real faithful irrep on \({\mathbb{R}^{4n}}\), which is also unique. The unique real faithful irrep of \({\mathbb{R}(n)}\) is the obvious one on \({\mathbb{R}^{n}}\), so the above comprises all real faithful irreps of \({\mathbb{K}(n)}\).
Since all Clifford algebras are isomorphic to a matrix algebra of the form \({\mathbb{K}(n)}\) or \({\mathbb{K}(n)\oplus\mathbb{K}(n)}\), every Clifford algebra has either one unique real faithful irrep, called the pinor rep, or two real unfaithful irreps on the same vector space, called the positive pinor rep and the negative pinor rep. Similarly, every complexified Clifford algebra has either one faithful or two unfaithful complex irreps, also called pinor reps, and as we saw previously, these are also irreps of the real Clifford algebra on the same complex vector space. Various sub-classes of these irreps have corresponding names that are used in physics:
- Dirac rep: for even \({n}\), the irrep of \({C\left(r,s\right)}\) on \({\mathbb{C}^{2^{n/2}}}\) given by the isomorphism \({C\mathbb{^{C}}(n)\cong\mathbb{C}\left(2^{n/2}\right)}\)
- For odd \({n}\), there are two irreps of \({C\left(r,s\right)}\) on \({\mathbb{C}^{2^{(n-1)/2}}}\) given by the isomorphism \({C\mathbb{^{C}}\left(n\right)\cong\mathbb{C}\left(2^{\left(n-1\right)/2}\right)\oplus\mathbb{C}\left(2^{\left(n-1\right)/2}\right)}\); these are also sometimes called Dirac reps
- Majorana rep: for \({r-s=0}\) or 2 mod 8, the irrep of \({C\left(r,s\right)}\) on \({\mathbb{R}^{2^{n/2}}}\) given by the isomorphism \({C\left(r,s\right)\cong\mathbb{R}\left(2^{n/2}\right)}\)
- For \({r-s=1}\) mod 8, there are two irreps of \({C\left(r,s\right)}\) on \({\mathbb{R}^{2^{\left(n-1\right)/2}}}\) given by the isomorphism \({C\left(r,s\right)\cong\mathbb{R}\left(2^{\left(n-1\right)/2}\right)\oplus\mathbb{R}\left(2^{\left(n-1\right)/2}\right)}\); these are also sometimes called Majorana reps
The even subalgebra \({C_{0}(r,s)\cong C(r,s-1)}\) and its complexification thus also have either a unique faithful irrep, called the spinor rep, or two unfaithful irreps on the same vector space, called the right-handed and left-handed chiral spinor reps (AKA reduced spinor, semi-spinor, or half-spinor reps). The above sub-classes of irreps then have names when they are applied to \({C_{0}\left(r,s\right)}\):
- Weyl rep: for even \({n}\), the two irreps of \({C_{0}\left(r,s\right)}\) on \({\mathbb{C}^{2^{\left(n-2\right)/2}}}\) given by the isomorphism \({C_{0}^{\mathbb{C}}\left(n\right)\cong C\mathbb{^{C}}\left(n-1\right)\cong\mathbb{C}\left(2^{\left(n-2\right)/2}\right)\oplus\mathbb{C}\left(2^{\left(n-2\right)/2}\right)}\)
- Majorana-Weyl rep: for \({r-s=0}\) mod 8, the two irreps of \({C_{0}\left(r,s\right)}\) on \({\mathbb{R}^{2^{\left(n-2\right)/2}}}\) given by the isomorphism \({C_{0}\left(r,s\right)\cong C\left(s,r-1\right)\cong\mathbb{R}\left(2^{\left(n-2\right)/2}\right)\oplus\mathbb{R}\left(2^{\left(n-2\right)/2}\right)}\)
Thus a pinor rep may be irreducible as a representation of the Clifford algebra, but reducible when restricting the action to the even subalgebra, decomposing into two chiral spinor irreps. Elements of the vector space acted on by either pinor or spinor reps are called spinors, and are prefixed by the rep name (e.g. Dirac spinor); chiral spinors are sometimes called semi-spinors or half-spinors, and the vector space of spinors is called the spinor space.
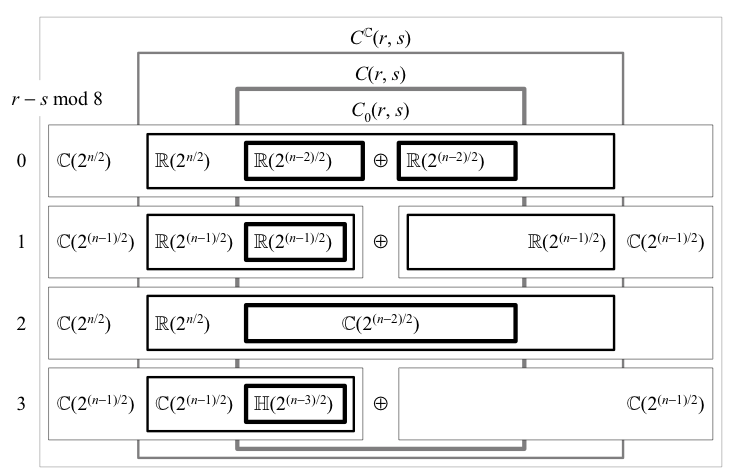
In summary, since all faithful irreps of Clifford algebras are directly related to their isomorphisms in terms of algebras \({\mathbb{K}(n)}\), we can use these matrix algebras to illustrate the above classification scheme.
The above depicts the classification of faithful Clifford algebra irreps using matrix algebra isomorphisms. For \({r-s}\) even (\({\Rightarrow n}\) even), \({C\mathbb{^{C}}\left(n\right)}\) has a Dirac rep, and \({C_{0}\mathbb{^{C}}(n)\cong C\mathbb{^{C}}(n-1)}\) splits into two Weyl reps. For \({r-s=0}\) or 2 mod 8, \({C\left(r,s\right)}\) has a real Majorana rep, and in the first case \({C_{0}\left(r,s\right)}\) splits into two Majorana-Weyl reps. The next four lines are obtained by using \({C\left(r,s\right)\otimes\mathbb{H}\left(2\right)\cong C\left(r,s+4\right)}\), so there are no further isomorphisms to \({gl(\mathbb{R})}\) and thus no further way to generalize Majorana reps.
This classification also reveals whether these various irreps are faithful. In even dimension, neither \({C\left(r,s\right)}\) nor \({C\mathbb{^{C}}\left(n\right)}\) is a direct sum, so the Dirac irrep is faithful. In odd dimension, for \({r-s=1}\) or 5 mod 8, \({C\mathbb{^{C}}\left(n\right)}\) is a direct sum but so is \({C\left(r,s\right)}\), so neither Dirac irrep is faithful; when \({r-s=3}\) or 7 mod 8, \({C\mathbb{^{C}}\left(n\right)}\) is a direct sum but \({C\left(r,s\right)}\) is not, and therefore the two Dirac irreps are faithful. The Majorana and Majorana-Weyl reps are isomorphisms, and hence are faithful iff they are not a direct sum. When \({r-s=0}\) mod 8, \({C_{0}\left(r,s\right)}\) is a direct sum \({\mathbb{R}\left(m\right)\oplus\mathbb{R}\left(m\right)}\) which sits in \({C\mathbb{^{C}}\left(n-1\right)\cong\mathbb{C}\left(m\right)\oplus\mathbb{C}\left(m\right)}\), where \({m\equiv2^{\left(n-2\right)/2}}\), so the Weyl irreps are unfaithful, as they are for \({r-s=4}\) mod 8. When \({r-s=2}\) mod 8 (including for \({C_{0}(3,1)}\)), \({C_{0}\left(r,s\right)\cong\mathbb{C}\left(m\right)}\) sits in \({\mathbb{C}\left(m\right)\oplus\mathbb{C}\left(m\right)}\), so the Weyl irreps are faithful, as they are for \({r-s=6}\) mod 8.