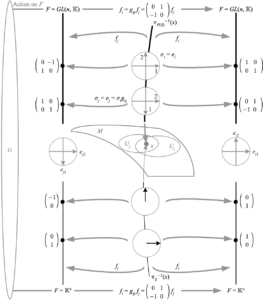
Given a vector bundle \({(E,M,\mathbb{K}^{n})}\), the frame bundle of \({E}\) is the principal \({GL(n,\mathbb{K})}\)-bundle associated to \({E}\), and is denoted \({F(E)\equiv(F(E),M,\pi,GL(n,\mathbb{K}))}\). The elements \({p\in\pi^{-1}(x)}\) are viewed as ordered bases of the internal space \({V_{x}\cong\mathbb{K}^{n}}\), which we denote
\(\displaystyle p\equiv e_{p}, \)
or \({e_{p\mu}}\) if operated on by a matrix in index notation. Each trivializing neighborhood \({U_{i}}\) is associated with a fixed frame \({e_{i}}\), which we take from the local trivializations in the vector bundle \({E}\), letting us define \({f_{i}\colon\pi^{-1}(x)\rightarrow GL(n,\mathbb{K})}\) by the matrix relation
\(\displaystyle e_{p}=e_{i}f_{i}(p). \)
In other words \({f_{i}(p)}\) is the matrix that transforms (as row vectors) the fixed basis \({e_{i}}\) into the basis element \({e_{p}}\) of \({F(E)}\); in particular, the identity section is
\(\displaystyle \sigma_{i}=f_{i}^{-1}(I)=e_{i}, \)
where \({I}\) is the identity matrix. If we again write vector components in these bases as \({v_{i}^{\mu}e_{i\mu}=v_{p}^{\mu}e_{p\mu}=v}\), then we have
\(\displaystyle v_{i}^{\mu}=f_{i}(p)^{\mu}{}_{\lambda}v_{p}^{\lambda}. \)
The left action of \({g_{ij}}\) is defined by \({f_{i}(p)=g_{ij}f_{j}(p)}\), and applying both sides to vector components \({v_{p}^{\mu}}\) we get
\(\displaystyle v_{i}^{\mu}=(g_{ij})^{\mu}{}_{\lambda}v_{j}^{\lambda}, \)
the same transition functions as in \({E}\). The transition functions can be viewed as changes of frame \({e_{j}=e_{i}g_{ij}}\), or gauge transformations, between the identity sections of \({F(E)}\) in \({U_{i}\cap U_{j}}\), i.e. this can be written as a matrix relation
\(\displaystyle \sigma_{j}=\sigma_{i}g_{ij}, \)
which as we see next is the usual right action of the transition functions on identity sections.
The above depicts how given a vector bundle \({E}\), we can construct an associated frame bundle \({F(E)}\). The elements of the fiber over \({x}\) in the frame bundle can be viewed as bases for the internal space, with the local trivialization acting as a choice of a fixed basis against which linear transformations generate these bases. These fixed bases are the same as those chosen in the corresponding local trivialization on the vector bundle, and are acted on by the same transition functions. Although denoted identically, the \({f_{i}}\) are those corresponding to each bundle.
| Δ Unlike with \({E}\), the frame is in fact part of the bundle \({F(E)}\), but vectors and vector components are not. The left action of \({g_{ij}}\) on the abstract fiber \({GL(n,\mathbb{K})}\) is equivalent to a transformation in the opposite direction from the fixed frame in \({U_{i}}\) to the fixed frame in \({U_{j}}\), which is a right action on the identity sections from \({\sigma_{i}=e_{i}}\) to \({\sigma_{j}=e_{j}}\). |
| Δ It is important to remember that the elements of \({\pi^{-1}(x)}\) in \({F(E)}\) are bases of the vector space \({V_{x}}\), and in a given trivializing neighborhood it is only the basis in the identity section that is identified with the basis underlying the vector components in the same trivializing neighborhood of \({E}\). |
The right action of \({g\in GL(n,\mathbb{K})}\) on \({\pi^{-1}(x)}\) is defined by \({f_{i}(g(p))=f_{i}(p)g}\), and applying both sides to \({e_{i}}\) from the right and using \({e_{p}=e_{i}f_{i}(p)}\) we immediately obtain
\(\displaystyle e_{g(p)}=e_{p}g, \)
so that the right action of the matrix \({g}\) is literally matrix multiplication from the right on the basis row vector \({p=e_{p\mu}}\). Alternative ways of writing this relation include
\(\displaystyle \begin{aligned}e_{g(p)\mu} & =e_{p\mu}g^{\mu}{}_{\lambda},\\ g(p) & =pg. \end{aligned} \)
In particular, if \({f_{i}(p)=g}\) then we have
\(\displaystyle p=e_{p}=e_{i}g=g(e_{i})=e_{g(e_{i})}. \)
| ◊ Note that since the right action on \({\pi^{-1}(x)}\) is by a fixed matrix, it acts as a transformation relative to each \({e_{p}}\), not as a transformation on the internal space \({V_{x}}\) in which all of the bases in \({\pi^{-1}(x)}\) live. As a concrete example, if \({g^{0}{}_{0}=1}\) and \({g^{\lambda\neq0}{}_{0}=0}\), then \({e_{g(p)0}=e_{p0}}\), meaning that the transformation \({p\mapsto g(p)}\) leaves the first vector of all bases in \({\pi^{-1}(x)}\) unaffected, regardless of that vector’s direction. This behavior contrasts with that of a transformation on \({V_{x}}\) itself, which as we will see in the next section is a gauge transformation. |