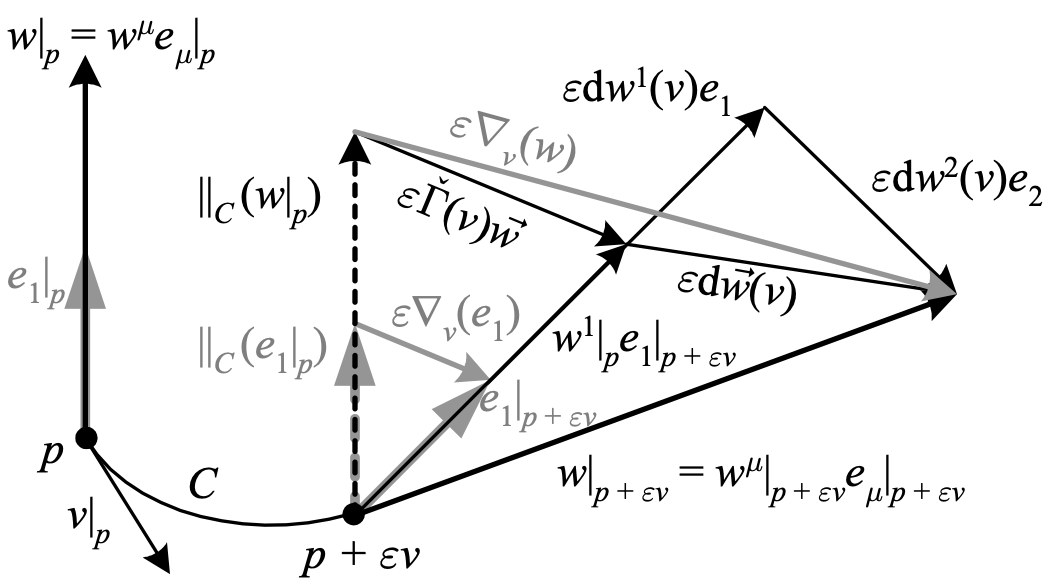
\({\nabla_{v}w}\) can be written in terms of \({\check{\Gamma}}\) by using the Leibniz rule for the covariant derivative with \({w^{\mu}}\) as frame-dependent functions:
\begin{aligned}\nabla_{v}w & =\nabla_{v}\left(w^{\mu}e_{\mu}\right)\\ & =v\left(w^{\mu}\right)e_{\mu}+w^{\mu}\nabla_{v}\left(e_{\mu}\right)\\ & =\mathrm{d}w^{\mu}\left(v\right)e_{\mu}+\check{\Gamma}\left(v\right)\vec{w}\\ & \equiv\mathrm{d}\vec{w}\left(v\right)+\check{\Gamma}\left(v\right)\vec{w} \end{aligned}
Here we again view \({\vec{w}}\) as a \({\mathbb{R}^{n}}\)-valued 0-form, so that \({\mathrm{d}\vec{w}\left(v\right)\equiv\mathrm{d}w^{\mu}\left(v\right)e_{\mu}}\). Thus \({\mathrm{d}\vec{w}\left(v\right)}\) is the change in the components of \({w}\) in the direction \({v}\), making it frame-dependent even though \({w}\) is not. Note that although \({\nabla_{v}w}\) is a frame-independent quantity, both terms on the right hand side are frame-dependent. This is depicted in the following figure.
The above depicts relationships between the frame, parallel transport, covariant derivative, and connection for a vector \({w}\) parallel to \({e_{1}}\) at a point \({p}\).
| ◊ The relation \({\nabla_{v}w=\check{\Gamma}\left(v\right)\vec{w}+\mathrm{d}\vec{w}\left(v\right)}\) can be viewed as roughly saying that the change in \({w}\) under parallel transport is equal to the change in the frame relative to its parallel transport plus the change in the components of \({w}\) in that frame. |
If the 1-form \({\Gamma^{\lambda}{}_{\mu}\left(v\right)}\) itself is written using component notation, we arrive at the connection coefficients
\(\displaystyle \Gamma^{\lambda}{}_{\mu\sigma}\equiv\Gamma^{\lambda}{}_{\mu}\left(e_{\sigma}\right)=\beta^{\lambda}\left(\nabla_{e_{\sigma}}e_{\mu}\right). \)
\({\Gamma^{\lambda}{}_{\mu\sigma}}\) thus measures the \({\lambda^{\mathrm{th}}}\) component of the difference between \({e_{\mu}}\) and its parallel transport in the direction \({e_{\sigma}}\).
| Δ This notation is potentially confusing, as it makes \({\Gamma^{\lambda}{}_{\mu\sigma}}\) look like the components of a tensor, which it is not: it is a derivative of the component of the frame indexed by \({\mu}\), and therefore is not only locally frame-dependent but also depends upon values of the frame at other points, so that it is not a multilinear mapping on its local arguments. Similarly, \({\mathrm{d}\vec{w}}\) looks like a frame-independent exterior derivative, but it is not: it is the exterior derivative of the frame-dependent components of \({w}\). |
| Δ The ordering of the lower indices of \({\Gamma^{\lambda}{}_{\mu\sigma}}\) is not consistent across the literature (e.g. [17] vs [15]). This is sometimes not remarked upon, possibly due to the fact that in typical circumstances in general relativity (a coordinate frame and zero torsion, to be defined here), the connection coefficients are symmetric in their lower indices. |
It is common to extend abstract index notation to be able to express the covariant derivative in terms of the connection coefficients as follows:
\begin{aligned}\nabla_{e_{\mu}}w & =\mathrm{d}w^{\lambda}\left(e_{\mu}\right)e_{\lambda}+\Gamma^{\lambda}{}_{\sigma}\left(e_{\mu}\right)w^{\sigma}e_{\lambda}\\
\Rightarrow\nabla_{a}w^{b}\equiv\left(\nabla_{e_{a}}w\right)^{b} & =e_{a}\left(w^{b}\right)+\Gamma^{b}{}_{ca}w^{c}\\
\Rightarrow\nabla_{a}w^{b} & =\partial_{a}w^{b}+\Gamma^{b}{}_{ca}w^{c}
\end{aligned}
Here we have also defined \({\partial_{a}f\equiv\partial_{e_{a}}f=\mathrm{d}f(e_{a})=e_{a}(f)}\), which is then extended to \({\partial_{v}f\equiv v^{a}\partial_{a}f}\). This notation is also sometimes supplemented to use a comma to indicate partial differentiation and a semicolon to indicate covariant differentiation, so that the above becomes
\(\displaystyle w^{b}{}_{;a}=w^{b}{}_{,a}+\Gamma^{b}{}_{ca}w^{c}. \)
The extension of index notation to derivatives has a number of potentially confusing aspects:
- \({\partial_{a}}\) written alone is not a 1-form, but \({\partial_{a}f}\) is, since the derivative is linear
- \({\partial^{a}\equiv g^{ab}\partial_{b}}\) is not the frame dual to \({\partial_{a}}\), which is \({\mathrm{d}x^{a}}\)
- Greek indices indicate only that a specific basis (frame) has been chosen ([16] pp. 23-26), but do not distinguish between a general frame, where \({\partial_{\mu}f\equiv\mathrm{d}f(e_{\mu})}\), and a coordinate frame, where \({\partial_{\mu}f\equiv\partial f/\partial x^{\mu}}\)
- \({\nabla_{a}}\) alone is not a 1-form, but since \({\nabla_{a}w^{b}\equiv(\nabla_{e_{a}}w)^{b}}\) and \({\nabla_{v}w}\) is linear in \({v}\), \({\nabla_{a}w^{b}}\) is in fact a tensor of type \({\left(1,1\right)}\); a more accurate notation might be \({(\nabla w)^{b}{}_{a}}\)
- \({w^{b}}\) in the expression \({\partial_{a}w^{b}\equiv\mathrm{d}w^{b}(e_{a})}\) is not a vector, it is a set of frame-dependent component functions labeled by \({b}\) whose change in the direction \({e_{a}}\) is being measured
- The above means that, consistent with the definition of the connection coefficients, we have \({\nabla_{a}e_{b}=0+e_{c}\Gamma^{c}{}_{ba}}\), since the components of the frame itself by definition do not change
- When using a coordinate frame based on curvilinear coordinates in Euclidean space, parallel transport is implicit in taking partial derivatives of vectors, resulting in the above being expressed as \({\partial_{\mu}e_{\lambda}=e_{\sigma}\Gamma^{\sigma}{}_{\lambda\mu}}\)
- As previously noted, neither \({\Gamma^{b}{}_{ca}}\) nor \({\Gamma^{b}{}_{ca}w^{c}}\) are tensors
We will nevertheless use this notation for many expressions going forward, as it is frequently used in general relativity.
| Δ It is important to remember that expressions involving \({\nabla_{a}}\), \({\partial_{a}}\), and \({\Gamma^{c}{}_{ba}}\) must be handled carefully, as none of these are consistent with the original concept of indices denoting tensor components. |
| Δ Some texts will distinguish between the labels of basis vectors and abstract index notation by using expressions such as \({(e_{i})^{a}}\). We will not follow this practice, as it makes difficult the convenient method of matching indexes in expressions such as \({\partial_{a}w^{b}\equiv\mathrm{d}w^{b}(e_{a})}\). |
| Δ If we choose coordinates \({x^{\mu}}\) and use a coordinate frame so that \({\partial_{\mu}\equiv\partial/\partial x^{\mu}}\), we have the usual relation \({\partial_{\mu}\partial_{\nu}f=\partial_{\nu}\partial_{\mu}f}\). However, this is not necessarily implied by the Greek indices alone, which only indicate that a particular frame has been chosen. For index notation in general, mixed partials do not commute, since \({\partial_{a}\partial_{b}f-\partial_{b}\partial_{a}f=e_{a}(e_{b}(f))-e_{b}(e_{a}(f))=[e_{a},e_{b}](f)=[e_{a},e_{b}]^{c}\partial_{c}f}\), which only vanishes in a holonomic frame. |