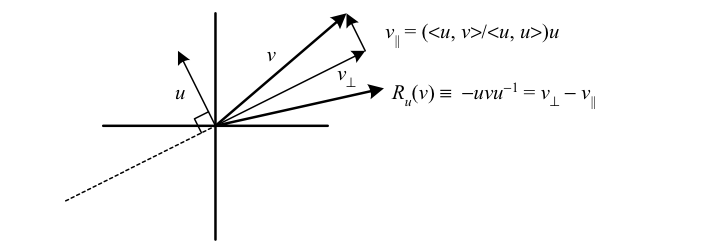
In the Clifford algebra, any “unit” vector, i.e. a vector \({u}\) with \({\left\langle u,u\right\rangle =\pm1}\), has inverse \({u^{-1}=u/\left\langle u,u\right\rangle =\pm u}\). It turns out that for any vector \({v}\), the quantity \({R_{u}(v)\equiv-uvu^{-1}}\) is the reflection of \({v}\) in the hyperplane orthogonal to the unit vector \({u}\).
We can see this by decomposing \({v}\) into a part \({v_{\Vert}=\left(\left\langle u,v\right\rangle /\left\langle u,u\right\rangle \right)u}\) that is parallel to \({u}\) and the remaining part \({v_{\perp}}\) that is orthogonal to \({u}\). Since parallel vectors commute, we have \({-uv_{\Vert}u^{-1}=-v_{\Vert}}\). In contrast, orthogonal vectors anti-commute, so that we have \({-uv_{\perp}u^{-1}=v_{\perp}}\), and thus
\(\displaystyle R_{u}\left(v\right)=-uvu^{-1}=-u\left(v_{\perp}+v_{\Vert}\right)u^{-1}=v_{\perp}-v_{\Vert}. \)
In the preceding figure, define \({\hat{v}_{\perp}}\) to be the unit vector perpendicular to \({u}\); then
\begin{aligned}u^{\prime} & \equiv u\cos\frac{\theta}{2}+\hat{v}_{\perp}\sin\frac{\theta}{2}\end{aligned}
is a vector rotated by \({\theta/2}\) from \({u}\). The combination of reflections using these two vectors yields a rotation of \({v}\) by \({\theta}\) in the \({u\wedge v}\) plane:
\begin{aligned}R_{\theta}\left(v\right) & =u^{\prime}uvuu^{\prime}\\
& =\left(u^{\prime}u\right)v\left(u^{\prime}u\right)^{-1}
\end{aligned}
Note that for infinitesimal \({\theta}\), we then have
\begin{aligned}u^{\prime}u & =1+\hat{v}_{\perp}u\theta/2\\
& =\exp\left(\hat{v}_{\perp}u\theta/2\right),
\end{aligned}
so that an infinitesimal rotation corresponds to the exponential of a bivector.