Most mathematical objects can be viewed as a set of elements along with a “structure.” In algebra this structure usually consists of equations that relate the elements to each other, while in geometry the focus is more on relations between subsets of the elements. For example \({\mathbb{Z}_{2}}\), the integers modulo 2, is defined by the two elements \({\{0,1\}}\) and the equations \({0+0=0,0+1=1+0=1,1+1=0}\).

We can also introduce the concept of mappings between sets with similar structures. Types of mappings include:

• Homomorphism: preserves the structure (e.g. a homomorphism \({\varphi}\) on \({\mathbb{Z}_{2}}\) satisfies \({\varphi(g+h)=\varphi(g)+\varphi(h)}\))
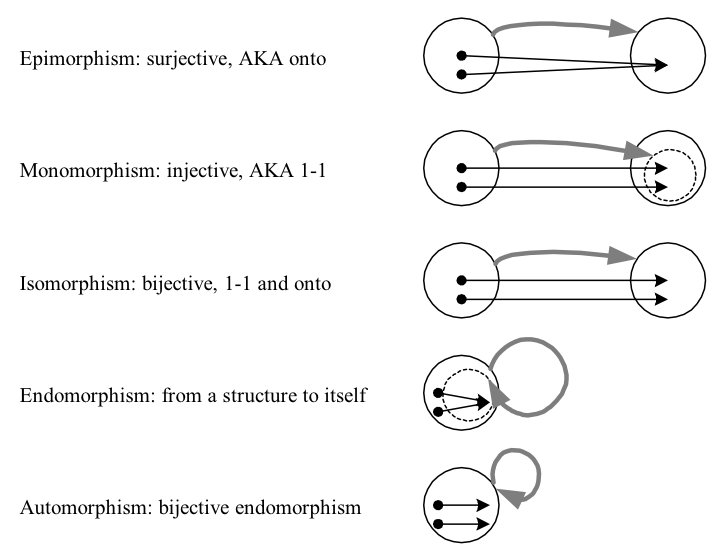
• Epimorphism: a homomorphism that is surjective (AKA onto)
• Monomorphism: a homomorphism that is injective (AKA one-to-one, 1-1, or univalent)
• Isomorphism: a homomorphism that is bijective (AKA 1-1 and onto); isomorphic objects are equivalent, but perhaps defined in different ways
• Endomorphism: a homomorphism from an object to itself
• Automorphism: a bijective endomorphism (an isomorphism from an object onto itself, essentially just a re-labeling of elements)

The concepts of sets and mappings can be generalized further, which takes us from set theory to category theory. In category theory, morphisms have generalized definitions which can in some cases be distinct from the ones we give, which are common in abstract algebra. An overview of the most basic ideas of category theory is presented in Appendix A. We will occasionally use category theory terminology (object, class, category, morphism and functor) to organize our presentation, but this topic is not necessary to understanding the content of the book.