Similarly, the \({k^{\textrm{th}}}\) exterior power of an n-dimensional vector space V is defined to be
\(\displaystyle \Lambda^{k}V\equiv V\wedge V\wedge\ldots\wedge V\qquad(k\:\mathrm{times}).\)
The exterior product is generalized to \({\Lambda^{k}V}\) by requiring the product to vanish if any two vector components are identical. This is equivalent to requiring the product to be completely anti-symmetric, i.e. to change sign under the exchange of any two vector components. Note that \({\Lambda^{k}V}\) thus automatically vanishes for \({k>n}\), since the \({(k+1)^{\textrm{th}}}\) component will have to be a linear combination of previous components, resulting in terms \({v\wedge v=0}\).
The exterior algebra (AKA Grassmann algebra, alternating algebra) is the tensor algebra modulo the relation \({v\wedge v\equiv0}\), and can be written as
\(\displaystyle \Lambda V\equiv\Sigma\Lambda^{k}V=\mathbb{R\oplus}\Lambda^{1}V\oplus\Lambda^{2}V\oplus\dotsb\oplus\Lambda^{n}V,\)
where \({n}\) is the dimension of \({V}\) (since \({\Lambda^{k}V}\) automatically vanishes for \({k>n}\)). The vector multiplication of the algebra is the exterior product \({\wedge}\), which applied to \({A\in\Lambda^{j}V}\) and \({B\in\Lambda^{k}V}\) gives \({A\wedge B\in\Lambda^{j+k}V}\) with the property
\(\displaystyle A\wedge B\equiv(-1)^{jk}B\wedge A. \)
If a pseudo inner product is defined on \({V}\), it can be naturally extended to any \({\Lambda^{k}V}\) by using the determinant: if \({A=v_{1}\wedge v_{2}\wedge\dotsb\wedge v_{k}}\), and \({B=w_{1}\wedge w_{2}\wedge\dotsb\wedge w_{k}}\), we define
\(\displaystyle \left\langle A,B\right\rangle \equiv\textrm{det}\left(\left\langle v_{i},w_{j}\right\rangle \right).\)
Note that this definition is also alternating, as it must for the inner product to be bilinear; i.e. exchanging two vectors in \({A}\) reverses the sign of both \({A}\) and \({\left\langle A,B\right\rangle }\). Also note that if \({\hat{e}_{\mu}}\) is an orthonormal basis for \({V}\) and \({A=a\hat{e}_{1}\wedge\dotsb\wedge\hat{e}_{k}}\), then \({\left\langle A,A\right\rangle =\pm a^{2}}\). The pseudo inner product can then be extended to a nondegenerate symmetric multilinear alternating form on all of \({\Lambda V}\) by defining it to be zero between elements from different exterior powers. In terms of the orthonormal \({\hat{e}_{\mu}}\),
\(\displaystyle \left\{ \hat{e}_{\mu_{1}}\wedge\dotsb\wedge\hat{e}_{\mu_{k}}\right\} _{1\leq\mu_{1} < \dotsb < \mu_{k}\leq n}\)
is an orthonormal basis for \({\Lambda^{k}V}\), and the union of such bases for \({k\leq n}\) is an orthonormal basis for \({\Lambda V}\).
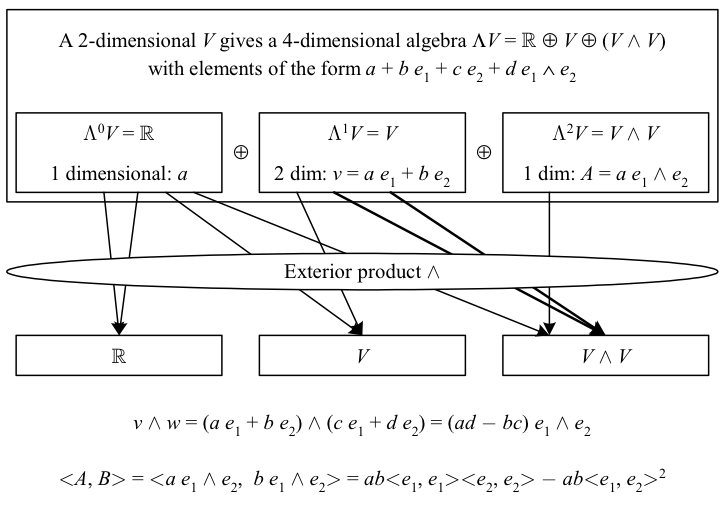
In describing a particular element of \({\Lambda V}\) we can unambiguously write \({+}\) instead of \({\oplus}\) and allow any zero terms to be omitted. A simple example can be helpful to keep in mind the concrete consequences of the exterior algebra’s abstract properties.
The above depicts the exterior algebra over a real 2-dimensional vector space. Exterior products not shown above vanish; the product indicated with bold arrows is elaborated by the first equation. The second equation calculates the inner product of two elements of \({\Lambda^{2}V}\) using the determinant.