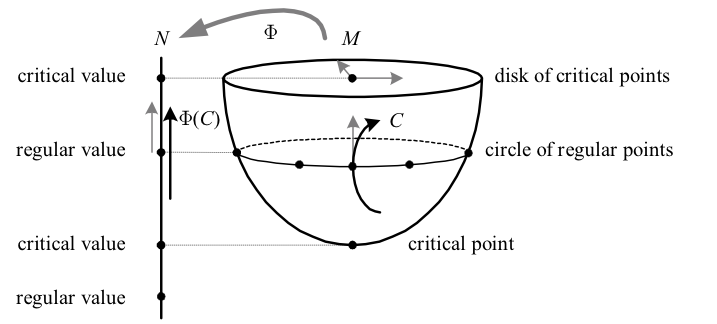
General mappings \({\Phi\colon M\to N}\) between manifolds classify points according to how they transform, and can be used to extract information about the manifolds:
- Regular point: \({p\in M}\) such that \({\mathrm{d}\Phi_{p}}\) maps \({T_{p}M}\) onto \({T_{\Phi(p)}N}\); if the map is not onto, \({p}\) is called a critical point
- Regular value: \({q\in N}\) such that \({\Phi^{-1}\left(q\right)}\) consists of all regular points or is empty; if \({\Phi^{-1}\left(q\right)}\) includes a critical point, \({q}\) is called a critical value
The above depicts the critical points of the height function \({\Phi}\) mapping a hollow bullet to its vertical component. The flat top and tip only have horizontal tangents, so that \({\mathrm{d}\Phi}\) is not onto. At a regular point, the tangent to a curve \({C\in M}\) is mapped to the tangent of the mapped curve \({\Phi\left(C\right)}\) via the Jacobian.
If all points in \({M}\) are regular then \({\Phi}\) is called a submersion. Sard’s theorem states that if \({\Phi}\) is sufficiently differentiable, almost all values are regular (we will not elaborate on “sufficient” and “almost” here). Morse theory uses these concepts to extract cell complex structures and homological information from a given manifold.