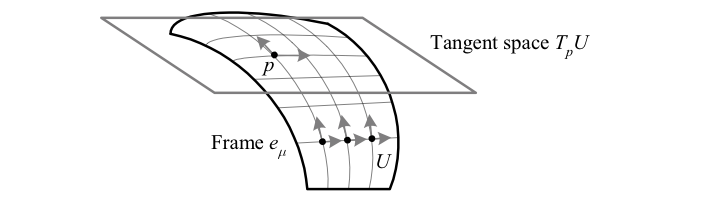
A frame \({e_{\mu}}\) on \({U\subset M^{n}}\) is defined to be a tensor field of bases for the tangent spaces at each point, i.e. \({n}\) linearly independent smooth vector fields \({e_{\mu}}\).
The concept of frame has a particularly large number of synonyms (although these terms sometimes imply that the frame is orthonormal), including comoving frame, repère mobile, vielbein, \({n}\)-frame, and \({n}\)-bein (where \({n}\) is the dimension). The dual frame, the \({1}\)-forms \({\beta^{\mu}}\) corresponding to a frame \({e_{\mu}}\), is also often simply called the frame.
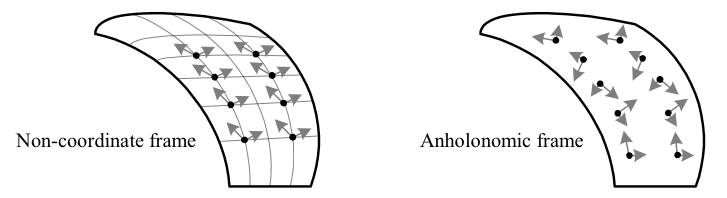
When using particular coordinates \({x^{\mu}}\), the frame \({e_{\mu}=\partial/\partial x^{\mu}}\) is called the coordinate frame (AKA coordinate basis or associated basis); any other frame is then called a non-coordinate frame. A holonomic frame is a coordinate frame in some coordinates (though perhaps not the ones being used); this condition is equivalent to requiring that \({\left[e_{\mu},e_{\nu}\right]=0}\), as we will see. An anholonomic frame is then a frame that cannot be derived from any coordinate chart in its region of definition. Using a non-coordinate frame suited to a specific problem is sometimes called the method of moving frames.
| Δ Note that the distinction between holonomic and coordinate frames as defined here is often not made. |
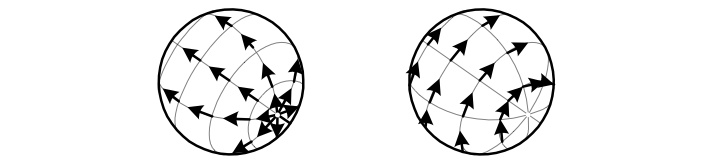
A frame cannot usually be globally defined on a manifold. A simple way to see this is by the example of the 2-sphere \({S^{2}}\). Any drawing of coordinate functions on a globe will have singularities, such as the north and south poles when using latitude and longitude; these are points where the associated coordinate frame will either be undefined or will vanish. In general, there is no non-zero smooth vector field that can be defined on \({S^{n}}\) for even \({n}\) (this is sometimes called the hedgehog theorem, AKA hairy ball theorem, coconut theorem).
The above depicts the hedgehog theorem for \({S^{2}}\), showing that any attempt to “comb the hair of a hedgehog” yields bald spots, in this case at the poles.
A manifold that can have a global frame defined on it is called parallelizable. Some facts regarding parallelizable manifolds include:
- All parallelizable manifolds are orientable (and therefore have a volume form), but as we saw with \({S^{2}}\) the converse is not in general true
- Any orientable 3-manifold \({M^{3}}\) is parallelizable \({\Rightarrow}\) any 4-manifold \({M^{3}\times\mathbb{R}}\) is parallelizable (important in the case of the spacetime manifold)
- Of the \({n}\)-spheres, only \({S^{1}}\), \({S^{3}}\), and \({S^{7}}\) are parallelizable (this can be seen to be related to \({\mathbb{C}}\), \({\mathbb{H}}\), and \({\mathbb{O}}\) being the only normed finite-dimensional real division algebras beyond \({\mathbb{R}}\))
- The torus (with any number of holes) is the only closed orientable surface with a non-zero smooth vector field