The Lie algebra associated with a matrix group is denoted by the same abbreviation as the Lie group, but with lowercase letters; e.g. the Lie algebra of \({GL(n,\mathbb{R})}\) is denoted \({gl(n,\mathbb{R})}\). \({gl(n,\mathbb{R})}\) is easily seen to be the set of all real \({n\times n}\) matrices under the Lie commutator, and in general the Lie algebra associated with a matrix group can be expressed as matrices with entries in the same division algebra as the matrix group.
| Δ It is important to remember that the multiplication operation on the matrices of a Lie algebra is that of the Lie commutator using matrix multiplication. |
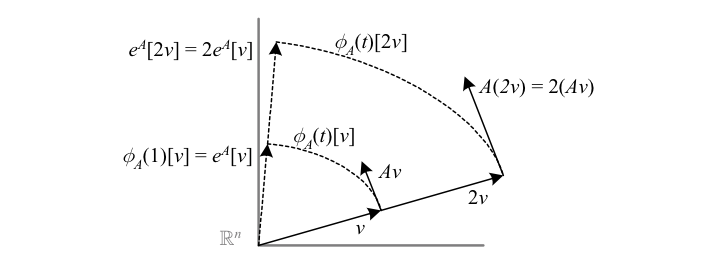
If an element of \({GL(n,\mathbb{R})}\) is considered to be a linear transformation on \({\mathbb{R}^{n}}\), an element of \({gl(n,\mathbb{R})}\) is an infinitesimal generator of a linear transformation. Thus an element \({A}\) of \({gl(n,\mathbb{R})}\) can be viewed as a vector field on \({\mathbb{R}^{n}}\) that “points in the direction of a linear transformation,” i.e. as a matrix it linearly transforms a vector \({v}\) into the tangent to the path in \({\mathbb{R}^{n}}\) traced by the one-parameter subgroup \({\phi_{A}\left(t\right)}\) applied to \({v}\).
| Δ This view of the element \({A\in gl(n,\mathbb{R})}\) as a vector field on \({\mathbb{R}^{n}}\) should not be confused with the view of \({A}\) as a vector field on \({GL(n,\mathbb{R})}\) as a submanifold of \({\mathbb{R}^{n^{2}}}\). |
An element of \({GL(n,\mathbb{R})}\) is a linear transformation on \({\mathbb{R}^{n}}\), while an element \({A}\) of the associated Lie algebra \({gl(n,\mathbb{R})}\) is a vector field on \({\mathbb{R}^{n}}\) that “points in the direction” of the element \({e^{A}\in GL\left(n,\mathbb{R}\right)}\).