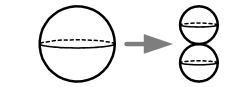
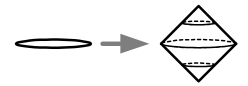
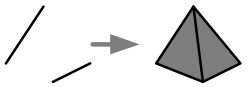
Another way to construct spaces is by combining them in various ways, as described in the following table. We denote the unit interval \({[0,1]}\) by \({I}\). \({X-Y}\) simply denotes the usual removal of a subset \({Y}\).

Operation	Example
Product:
\({X\times Y=}\) all points \({\left(x,y\right)}\) with \({x\in X}\), \({y\in Y}\)
Example: \({S^{1}\times S^{1}=T^{2}}\), the torus
Wedge sum:
\({X\vee Y}\) identifies a point from each space
Example: \({S^{1}\vee S^{1}=}\) the figure eight
Quotient:
\({X/A}\) collapses \({A\subset X}\) to a point
Example: \({S^{2}/S^{1}=S^{2}\vee S^{2}}\)
Suspension:
\({SX=}\) the quotient of \({X\times I}\) with \({X\times\left\{ 0\right\} }\) and \({X\times\left\{ 1\right\} }\) collapsed to points
Example: \({SS^{1}=S^{2}}\)
Join:
\({X*Y=}\) all line segments from \({X}\) to \({Y}\); more precisely, \({X\times Y\times I}\) with \({X\times Y\times\left\{ 0\right\} }\) collapsed to \({X}\), \({X\times Y\times\left\{ 1\right\} }\) to \({Y}\)
Example: \({I*I=}\) solid tetrahedron

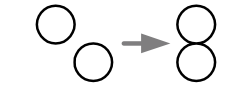
In the case of two disjoint connected \({n}\)-manifolds \({X}\) and \({Y}\), we can also define the connected sum \({X\#Y}\), obtained by removing the interiors of closed \({n}\)-balls from each and identifying the resulting boundary spheres.

The above depicts the connected sum \({S^{2}\#S^{2}=S^{2}}\).

Some facts about combining spheres are:

• If the product \({X\times Y=S^{n}}\) then one of the spaces is a point
• The quotient \({S^{n}/S^{n-1}=S^{n}\vee S^{n}}\) yields a wedge sum
• The suspension \({SS^{n}=S^{n+1}}\)
• The join \({S^{n}*S^{m}=S^{m+n+1}}\)
• The connected sum of \({n}\)-dimensional manifolds \({M\#S^{n}=M}\)