In general, multilinear mappings from a vector space to scalars are called “forms.” Here we define some forms with regard to the real vector space \({\mathbb{R}^{n}}\); more general definitions may exist in more general settings.
A form is completely symmetric if it is invariant under exchange of any two vector arguments; it is completely anti-symmetric (AKA alternating) if it changes sign under such an exchange. Some classes of forms include:
- Bilinear form: a bilinear map from two vectors to \({\mathbb{R}}\)
- Multilinear form: generalizes the above to take any number of vectors
- Quadratic form: equivalent to a symmetric bilinear form: a quadratic form is a homogeneous polynomial of degree two, i.e. every term has the same number of variables, with no power greater than 2; by considering the variables components of a vector, the polarization identity gives a 1-1 correspondence with symmetric bilinear forms.
- Algebraic form: generalization of the above to arbitrary degree; equivalent to a completely symmetric multilinear form
- 2-form: an anti-symmetric bilinear form
- Exterior form: a completely anti-symmetric multilinear form; exterior forms will be revisited from a different perspective in a subsequent section.
A real inner product is thus a positive definite quadratic form, and is the generalization to arbitrary dimension of the geometrically defined dot product in \({\mathbb{R}^{3}}\). Below we summarize the relationships between various forms.
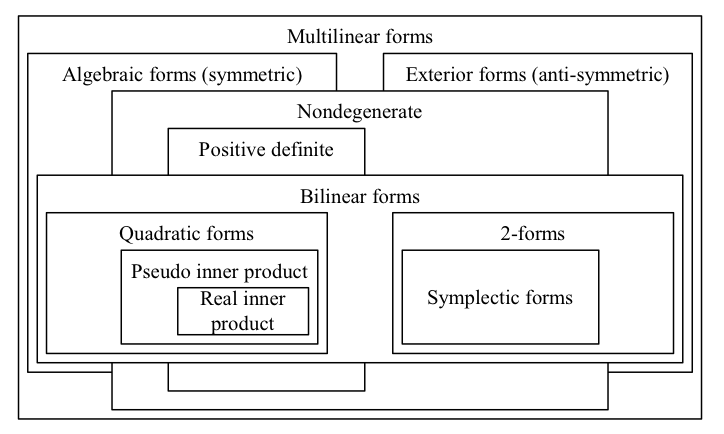
| ◊ The above is an Euler diagram, where the spatial relationships of the boxes indicate their relationships as sets (i.e. intersection, subset, disjoint). We will use these frequently in summarizing the relationships between mathematical concepts. |