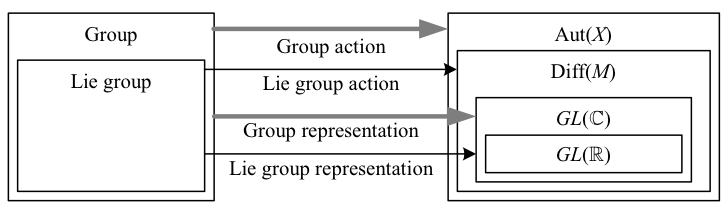
A group representation (AKA rep, linear representation) is a linear group action on a real or complex vector space \({V}\), i.e. a homomorphism \({\rho\colon G\to GL(V)}\) from \({G}\) to the Lie group of linear invertible automorphisms of the manifold \({V=\mathbb{R}^{n}}\) or \({\mathbb{C}^{n}}\). We can choose a basis of \({V}\) to get a isomorphism from \({GL(V)}\) to \({GL(n,\mathbb{R})}\) or \({GL(n,\mathbb{C})}\), in which case the representation is called a matrix representation. For a matrix rep, the transpose switches left and right actions like the inverse, as does an action by the matrix on row vectors instead of column vectors; in particular, a left matrix rep on vector components \({\left(v^{\mu}\right)^{\prime}=g^{\mu}{}_{\lambda}v^{\lambda}}\) is equivalent to a left action

\(\displaystyle e_{\mu}^{\prime}=(g^{-1})^{\lambda}{}_{\mu}e_{\lambda}=\begin{bmatrix}e_{1} & \cdots & e_{n}\end{bmatrix}\left[g^{-1}\right] \)

on the basis, since the inverse of the matrix acts on a row vector. The \({G}\)-space \({V}\) is called a representation space, and an equivariant linear map between representation spaces of the same group is called an intertwiner (AKA intertwining map).

Now, a group representation \({\rho\colon G\to GL(V)}\), being a homomorphism, satisfies \({\rho\left(gh\right)=\rho\left(g\right)\rho\left(h\right)}\). Similarly, an algebra representation of an associative algebra \({\mathfrak{a}}\) is defined to be a linear homomorphism \({\rho\colon\mathfrak{a}\to gl\left(V\right)}\), e.g. for scalar \({a}\) and vectors \({A,B,C}\) in \({\mathfrak{a}}\), we require that \({\rho\left(aA+BC\right)=a\rho\left(A\right)+\rho\left(B\right)\rho\left(C\right)}\). An algebra representation is also referred to as a G-module, or just a module, since if we ignore scalars in both \({V}\) and \({\mathfrak{a}}\), \({V}\) acted on by \({\mathfrak{a}}\) can be viewed as a module with vectors in the abelian group \({V}\) and scalars in the ring \({\mathfrak{a}}\).

We can now use the Lie commutator to define the related Lie algebra representation of a Lie algebra \({\mathfrak{g}}\) as a smooth linear homomorphism \({\rho\colon\mathfrak{g}\to gl\left(V\right)}\), i.e. we require \({\rho\left(\left[A,B\right]\right)=\rho\left(A\right)\rho\left(B\right)-\rho\left(B\right)\rho\left(A\right)}\). Note that a Lie algebra derived from a real Lie group is by definition a real vector space, since it lies in the tangent space of a real manifold; thus the scalar field in such a Lie algebra, even if defined by complex matrices, is the field of reals.