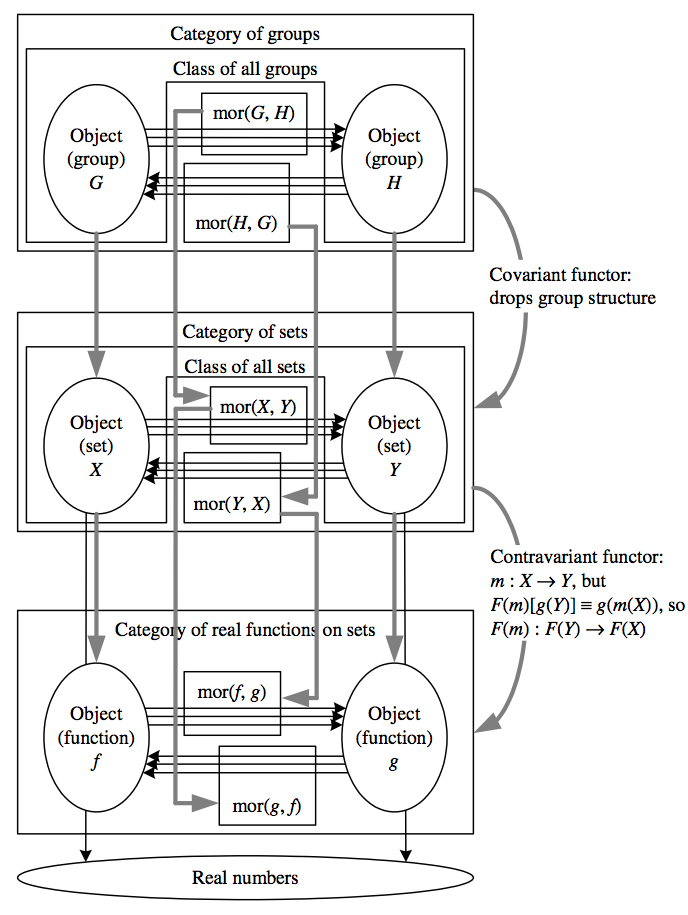
As described so far, category theory has essentially provided an abstract generalization of sets and mappings that ignores elements and thus can be used for diverse constructs. The real power of categories comes in the next step, in which we “move up a level” and define mappings between entire categories.
- Covariant functor: a mapping \({F}\) between categories \({C}\) and \({D}\) such that \({\forall X\in C}\), \({F(X)\in D}\), and \({\forall m\in\textrm{mor}(X,Y)}\), \({F(m)\in\textrm{mor}\left(F(X),F(Y)\right)}\), with \({F(\mathbf{1}_{X})=\mathbf{1}_{F(X)}}\) and \({F(n\circ m)=F(n)\circ F(m)}\)
- Contravariant functor: A “reversing” functor with properties as above, except that \({F(m)\in\textrm{Mor}\left(F(Y),F(X)\right)}\) and \({F(n\circ m)=F(m)\circ F(n)}\), i.e. a contravariant functor “flips the direction of morphisms”
To get a concrete sense of how functors work, we give an example that assumes familiarity with groups.
| Δ It should be emphasized that although we are using sets and mappings as examples of objects and morphisms, category theory can be used as a tool to illuminate and compare many dissimilar structures that otherwise would be difficult to relate to each other. |
Category theory can be used to generalize many other concepts; for example, the types of mappings in the figure on mappings defined in terms of set elements have generalized definitions in category theory, as do the operations in the section on combining algebraic objects.