For a Lie group \({G}\), the inner automorphism \({\phi_{g}\colon G\to G}\) induced by a fixed \({g\in G}\) is defined by \({h\mapsto ghg^{-1}}\), and can be viewed as an action of \({G}\) on itself. At the identity \({e}\) we then have the map \({\left(\mathrm{d}\phi_{g}\right)\left|_{e}\colon\mathfrak{g}\to\mathfrak{g}\right.}\). The adjoint representation \({\textrm{Ad}\colon G\to GL\left(\mathfrak{\mathfrak{g}}\right)}\) represents \({G}\) on \({\mathfrak{g}}\), and for \({A\in\mathfrak{g}}\) is defined by \({g_{\textrm{Ad}}\left(A\right)\equiv\left(\mathrm{d}\phi_{g}\right)\left|_{e}\left(A\right)\right.}\); it is often denoted \({\textrm{Ad}_{g}A}\). Using the exponential map, one can show that \({\textrm{exp}\left(tg_{\textrm{Ad}}\left(A\right)\right)=g\textrm{exp}\left(tA\right)g^{-1}}\). If \({G}\) is a matrix group, so that \({g}\) and \({A}\) are both matrices, the adjoint representation is simply the similarity transformation \({g_{\textrm{Ad}}(A)=gAg^{-1}}\).

The adjoint representation also sometimes refers to the representation of the Lie algebra \({\mathfrak{g}}\) on itself defined by the differential of \({\textrm{Ad }}\) at the identity: \({\textrm{ad}\equiv(\mathrm{d}\textrm{Ad})\left|_{e}\colon\mathfrak{g}\to gl\left(\mathfrak{g}\right)\right.}\). It can easily be shown that for a given \({A\in\mathfrak{g}}\), \({A_{\textrm{ad}}}\) is just the Lie derivative \({A_{\textrm{ad}}\left(B\right)=L_{A}\left(B\right)=\left[A,B\right]}\).

The trivial representation maps all of \({G}\) to the identity on a one-dimensional vector space; this representation is irreducible, and the corresponding Lie algebra representation maps all of \({\mathfrak{g}}\) to \({0}\).

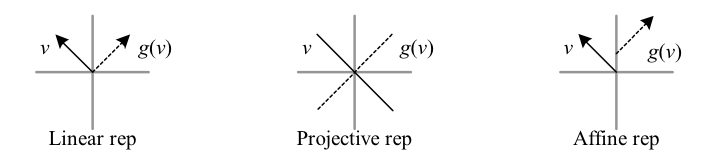
Closely related to linear representations are projective representations and affine representations, homomorphisms from \({G}\) to \({\textrm{Aut}(X)}\) where \({X}\) is a projective or affine space. Recall that a projective space is obtained from a vector space by taking all lines through the origin, i.e. by identifying scalar multiples of vectors. We can then view a projective representation as mapping each group element to an automorphism of a vector space \({V}\) “ignoring vector length.” An affine space is defined as a set on which a vector space acts freely and transitively as an additive group. Thus any two points in an affine space can be identified with the vector whose action relates them; i.e. an affine space “ignores the origin,” so that vectors are defined between any two points, even if one is not the origin. In particular, a group representation that maps each group element to an automorphism on \({V}\) that is an affine map (AKA inhomogeneous transformation), the sum of a linear and constant map, is an affine representation.