Nothing we have done so far has required the spaces of a fiber bundle to be manifolds; if they are, then we require the bundle projections \({\pi}\) to be (infinitely) differentiable and \({\pi^{-1}(x)}\) to be diffeomorphic to \({F}\), resulting in a smooth bundle. A smooth G-bundle then has a structure group \({G}\) which is a Lie group, and whose elements correspond to diffeomorphisms of \({F}\).
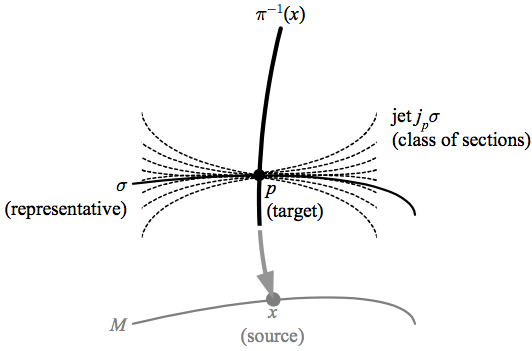
If we consider a local section \({\sigma}\) of a smooth fiber bundle \({(E,M,\pi,F)}\) with \({\sigma(x)=p}\), the equivalence class of all local sections that have both \({\sigma(x)=p}\) and also the same tangent space \({T_{p}\sigma}\) is called the jet \({j_{p}\sigma}\) with representative \({\sigma}\). We can also require that further derivatives of the section match the representative, in which case the order of matching derivatives defines the order of the jet, which is also called a k-jet so that the above definition would be that of a 1-jet. \({x}\) is called the source of the jet and \({p}\) is called its target. With some work to transition between local sections, one can then form a jet manifold by considering jets with all sources and representative sections, which becomes a jet bundle by considering jets to be fibers over their source.
The above depicts a jet with representative \({\sigma}\), source \({x}\), and target \({p}\).