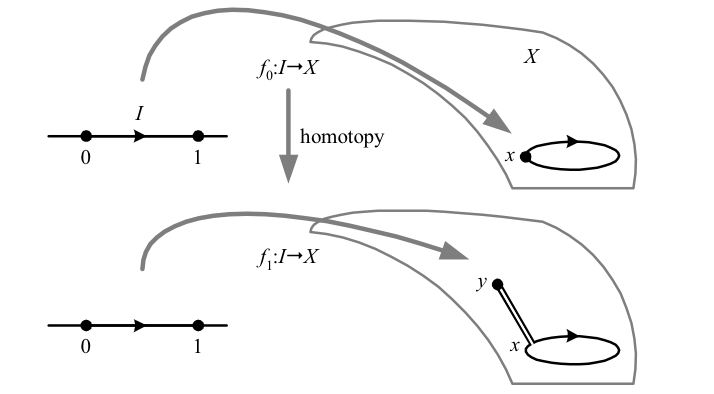
The simplest homotopy group is the fundamental group \({\pi_{1}\left(X\right)}\), which counts how many ways a loop can be mapped into a path-connected space \({X}\). More precisely, we define \({\pi_{1}\left(X,x\right)}\) to be the set of all homotopy classes of parameterized loop mappings that begin and end at a basepoint \({x}\). For a path-connected space we can add a path from \({x}\) to any other point and back as part of the loop, so that \({\pi_{1}\left(X,x\right)}\) is independent of \({x}\) and is written \({\pi_{1}\left(X\right)}\).
The above shows that for a path-connected space \({X}\), every loop with basepoint \({x}\) is homotopic to a loop with basepoint \({y}\), so that \({\pi_{1}\left(X,x\right)=\pi_{1}\left(X,y\right)=\pi_{1}\left(X\right)}\).
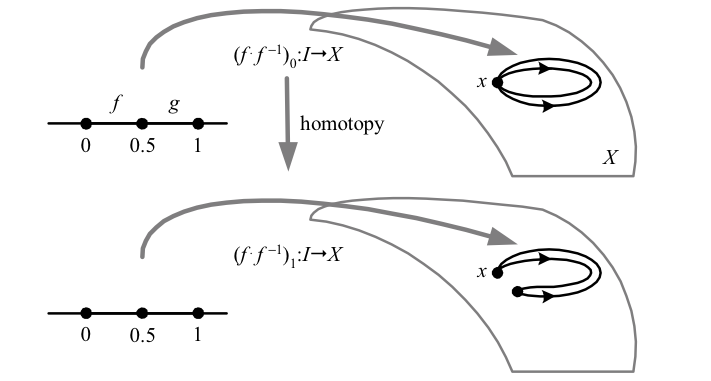
\({\pi_{1}\left(X\right)}\) becomes a group by defining multiplication as the composition of loop paths from a given basepoint. Technically, this is implemented by dividing the line segment \({I}\) in half, and applying the first mapping \({f}\) to the first half segment, \({g}\) to the second half. Note that this means that homotopies of \({fg}\) may abandon the midway mapping to the basepoint; for example, the inverse of a path is simply the same path traversed backwards.
Homotopies of loop products \({h=f\cdot g}\) are only required to keep the endpoints of \({h}\) mapped to the basepoint, allowing the midpoint \({f_{0.5}=g_{0.5}}\) to abandon the basepoint. Above we have \({g=f^{-1}}\), the inverse of \({f}\), in which case the midpoint leaving the basepoint results in the product \({f\cdot f^{-1}}\) retracting to a point.
So for example \({\pi_{1}\left(S^{1}\right)=\mathbb{Z}}\), since a loop can be mapped around the circle any number of times in either direction. For the figure eight \({S^{1}\vee S^{1}}\), a loop mapped around one circle cannot be homotopically altered to go around the other. Thus each homotopically distinct map can be viewed as a “word” with each “letter” an integer number of loops around each circle, i.e. we arrive at the free product \({\pi_{1}\left(S^{1}\vee S^{1}\right)=\mathbb{Z}*\mathbb{Z}}\). This example also shows that in general \({\pi_{1}}\) is non-abelian, unlike \({H_{1}}\) and as we will see below unlike all other \({\pi_{n}}\). In fact, \({\pi_{1}}\) is very general indeed: for any arbitrary group \({G}\) one can construct a space \({X}\) for which \({\pi_{1}\left(X\right)=G}\).
A path-connected space with trivial fundamental group is called simply connected. The name reflects the fact that in such a space there is only one homotopically distinct way to form a path between any two points.
| Δ Note that there are other definitions of “simply connected” in use; some do not require the space to be connected. |