Here we define the special vector fields that give Lie groups an associated Lie algebra. The left translation mapping \({L_{g}(h)\equiv gh}\) is a diffeomorphism on \({G}\), as is right translation \({R_{g}(h)\equiv hg}\). A left-invariant vector field \({A}\) then satisfies
\(\displaystyle \mathrm{d}L_{g}\left(\left.A\right|_{h}\right)=\left.A\right|_{L_{g}\left(h\right)}=\left.A\right|_{gh} \)
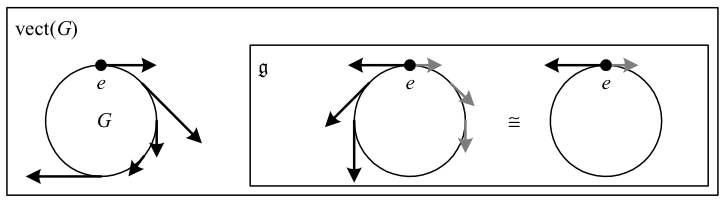
for any \({g}\) and \({h}\). In words, the vector field at any point can be obtained by the left translation of its value at any other point. Thus the vector field is invariant under a left translation diffeomorphism. In particular, a left-invariant vector field is then completely determined by its value at the identity.
The left-invariant vector fields on \({G}\) under the Lie commutator form its associated Lie algebra \({\mathfrak{g}}\) (which is also isomorphic to the right-invariant vector fields). Since each left-invariant vector field is uniquely determined by its value at the identity element (point) \({e}\), \({\mathfrak{g}}\) is isomorphic (as a vector space) to the tangent space \({T_{e}G}\), which of course has the same dimension as \({G}\). The elements of the Lie algebra \({\mathfrak{g}\cong T_{e}G}\) are often called the infinitesimal generators of \({G}\).
The above depicts the Lie group \({G}\) of rotations of a circle, which has an associated Lie algebra \({\mathfrak{g}\cong\mathbb{R}}\).
We can also define left-invariant forms by demanding invariance under left translated vector arguments, i.e. we require \({L_{g}^{*}\varphi=\varphi}\) where \({L_{g}^{*}}\) is the pullback. As with left-invariant vectors, left-invariant forms are uniquely determined by their value at the identity. The term Maurer-Cartan form can be used to refer to left-invariant 1-forms in general, a particular basis of left-invariant 1-forms, or a \({\mathfrak{g}}\)-valued 1-form that is the identity on left-invariant vector fields.
If we choose a basis of left-invariant 1-forms \({\alpha^{\mu}}\) (the dual to a basis of \({\mathfrak{g}}\)), we can construct a left-invariant volume form \({\alpha^{1}\wedge\dotsb\wedge\alpha^{n}}\) called a left Haar measure. A volume form constructed from a basis of right-invariant 1-forms is called a right Haar measure, and if it is bi-invariant, i.e. both left- and right-invariant, it is simply called a Haar measure. Haar measures allow one to construct integrals on \({G}\) that are invariant under left and/or right translation diffeomorphisms.