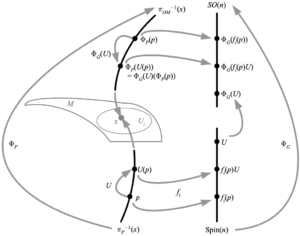
A spin structure on an orientable Riemannian manifold \({M}\) is a principal bundle map
\(\displaystyle \Phi_{P}\colon(P,M^{n},\mathrm{Spin}(n))\rightarrow(OM,M^{n},SO(n)) \)
from the spin frame bundle (AKA bundle of spin frames) \({P}\) to the orthonormal frame bundle \({OM}\) with respect to the double covering map \({\Phi_{G}\colon\mathrm{Spin}(n)\rightarrow SO(n)}\). The equivariance condition on the bundle map is then \({\Phi_{P}(U(p))=\Phi_{G}(U)(\Phi_{P}(p))}\), so that the right action of a spinor transformation \({U\in\mathrm{Spin}(n)}\) on a spin basis corresponds to the right action of a rotation \({\Phi_{G}(U)}\) on the corresponding orthonormal basis \({\Phi_{P}(p)}\). On a time and space orientable pseudo-Riemannian manifold, a spin structure is a principal bundle map with respect to the double covering map \({\Phi_{G}\colon\mathrm{Spin}(r,s)^{e}\rightarrow SO(r,s)^{e}}\) (except in the case \({r=s=1}\), which is not a double cover).
The above depicts the spin structure, a principal bundle map that gives a global 2-1 mapping from the fibers of the spin frame bundle to the fibers of the orthonormal frame bundle. The existence of a spin structure means that a change of frame can be smoothly and consistently mapped to changes of spin frame, permitting the existence of spinor fields.
If a spin structure exists for \({M}\), then \({M}\) is called a spin manifold (one also says \({M}\) is spin; sometimes a spin manifold is defined to include a specific spin structure). Any manifold that can be defined with no more than two coordinate charts is then spin, and therefore any parallelizable manifold and any \({n}\)-sphere is spin. As we will see, the existence of spin structures can be related to characteristic classes. It also can be shown that any non-compact spacetime manifold with signature \({(3,1)}\) is spin iff it is parallelizable. Finally, a vector bundle \({(E,M^{n},\mathbb{C}^{m})}\) associated to the spin frame bundle \({(P,M,\mathrm{Spin}(r,s)^{e})}\) under a rep of \({\mathrm{Spin}(r,s)^{e}}\) on \({\mathbb{C}^{m}}\) is called a spinor bundle, and a section of this bundle is a spinor field on \({M}\).
For a charged spinor field taking values in \({U(1)\otimes\mathbb{C}^{m}}\), where \({\mathbb{C}^{m}}\) is acted on by a rep of \({\mathrm{Spin}(r,s)^{e}}\), the action of \({(e^{i\theta},U)\in U(1)\times\mathrm{Spin}(r,s)^{e}}\) and \({(-e^{i\theta},-U)}\) are identical, so that the structure group is reducible to
\(\displaystyle \begin{aligned}\mathrm{Spin^{\mathbb{\mathit{c}}}}(r,s)^{e} & \equiv U(1)\times_{\mathbb{Z}_{2}}\mathrm{Spin}(r,s)^{e}\\ & \equiv\left(U(1)\times\mathrm{Spin}(r,s)^{e}\right)/\mathbb{Z}_{2}, \end{aligned} \)
where the quotient space collapses all points in the product space which are related by changing the sign of both components. The superscript refers to the circle \({U(1)}\). A spinc structure on an orientable pseudo-Riemannian manifold \({M}\) is then a principal bundle map
\(\displaystyle \Phi_{P}\colon(P,M^{n},\mathrm{Spin^{\mathbb{\mathit{c}}}}(r,s)^{e})\rightarrow(OM,M^{n},SO(r,s)^{e}) \)
with respect to the double covering map \({\Phi_{G}\colon\mathrm{Spin^{\mathbb{\mathit{c}}}}(r,s)^{e}\rightarrow SO(r,s)^{e}}\). For spinor matter fields that take values in \({V\otimes\mathbb{C}^{m}}\) for some internal space \({V}\) with structure (gauge) group \({G}\) with \({\mathbb{Z}_{2}}\) in its center (e.g. a matrix group where the negative of every element remains in the group), we can analogously define a spinG structure. It can be shown (see [1]) that spinG structures exist on any four dimensional \({M}\) if such a \({G}\) is a compact simple simply connected Lie group, e.g. \({SU(2i)}\); therefore the spacetime manifold has no constraints due to spin structure in the standard model, or in any extension that includes \({SU(2i)}\) gauged spinors.