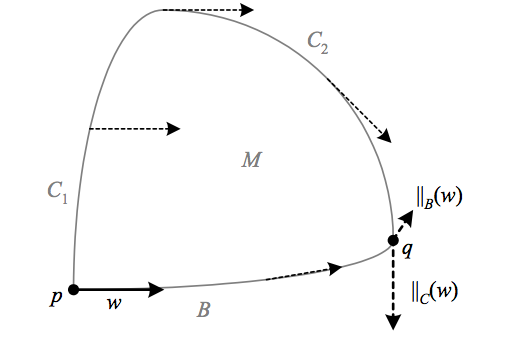
By definition, for a vector \({w}\) at a point \({p}\) of an \({n}\)-dimensional manifold \({M}\), parallel transport assigns a vector \({\parallel_{C}\left(w\right)}\) at another point \({q}\) that is dependent upon a specific path \({C}\) in \({M}\) from \({p}\) to \({q}\).

To see that this dependence upon the path matches our intuition, we can consider a vector transported in what we might consider to be a “parallel” fashion along the edges of an eighth of a sphere. In this example, the sphere is embedded in \({\mathbb{R}^{3}}\) and the concept of “parallel” corresponds to incremental vectors along the path having a projection onto the original tangent plane that is parallel to the original vector.

The above depicts how a vector \({w}\) transported in what we intuitively consider to be a “parallel” way along two different paths (\({B}\) and \({C=C_{1}+C_{2}}\)) on a surface results in two different vectors.

The parallel transporter is therefore a map \({\parallel_{C}\colon T_{p}M\to T_{q}M}\), where \({C}\) is a curve in \({M}\) from \({p}\) to \({q}\). To match our intuition we also require that this map be linear (i.e. parallel transport is assumed to preserve the vector space structure of the tangent space); that it be the identity for vanishing \({C}\); that if \({C=C_{1}+C_{2}}\) then \({\parallel_{C}=\parallel_{C_{2}}\parallel_{C_{1}}}\); and that the dependence on \({C}\) be smooth (this is most easily defined in the context of fiber bundles, which we will cover in a later chapter). If we then choose a frame on \({U\subset M}\), we have bases for each tangent space that provide isomorphisms \({T_{p}U\cong\mathbb{R}^{n}}\), \({T_{q}U\cong\mathbb{R}^{n}}\). Thus the parallel transporter can be viewed as a map \({\parallel^{\lambda}{}_{\mu}\colon\left\{ C\right\} \to GL\left(n,\mathbb{R}\right)}\) from the set of curves on \({U}\) to the Lie group \({GL\left(n,\mathbb{R}\right)}\); however, it is important to note that the values of \({\parallel^{\lambda}{}_{\mu}}\) depend upon the choice of frame.