On a smooth bundle with connection, the exterior covariant derivative gives us a definition for the curvature of the Ehresmann connection, the horizontal vector-valued 2-form
\(\displaystyle \vec{R}\equiv\mathrm{D}\vec{\Gamma}. \)
Recall that previously we saw that the analog of the above equation on \({M}\) itself did not hold. The horizontal tangent spaces of \({\vec{\Gamma}}\) define a foliation of the bundle iff this curvature vanishes.
On a smooth principal bundle with connection \({(P,M,G)}\), the curvature of the principal connection is the horizontal \({\mathfrak{g}}\)-valued 2-form
\(\displaystyle \check{R}_{P}\equiv \mathrm{D}\check{\Gamma}_{P}. \)
Since \({\check{\Gamma}_{P}}\) is vertical, this can be written
\(\displaystyle \begin{aligned}\check{R}_{P}\left(v,w\right) & =-\check{\Gamma}_{P}\left(\left[v^{⦵},w^{⦵}\right]\right)\\ \Rightarrow\mathrm{d}\rho\left(\check{R}_{P}\left(v,w\right)\right)\left|_{p}\right. & =-\left[v^{⦵},w^{⦵}\right]^{⌽}, \end{aligned} \)
so that the curvature of the principal connection is the element of \({\mathfrak{g}}\) corresponding to the vertical component of the Lie bracket of the horizontal components of its arguments.
On a frame bundle, we associate the horizontal tangent space with parallel transport, and the curvature is the “infinitesimal linear transformation between parallel transport in opposite directions around the boundary of the horizontal hypersurface defined by its arguments,” or equivalently the “infinitesimal linear transformation associated with the vertical component of the negative Lie bracket of the horizontal components of its arguments.” The curvature on \({M}\) can be recovered using identity sections \({\sigma_{i}}\) as with the connection to yield
\(\displaystyle \check{R}_{i}\equiv\sigma_{i}^{*}\check{R}_{P}, \)
where again to avoid clutter we write \({\check{R}_{i}}\) instead of \({\left(\check{R}_{A}\right)_{i}}\).
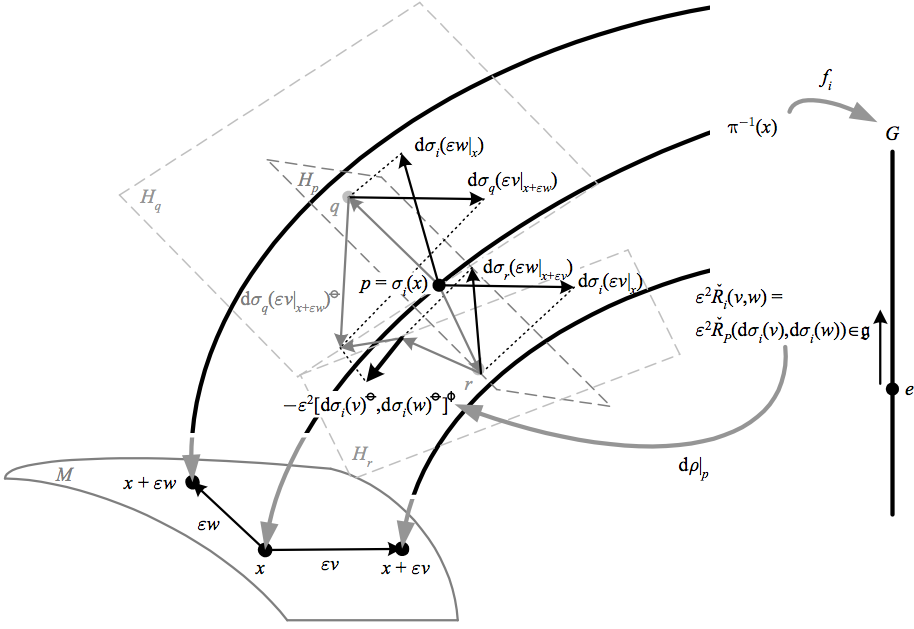
The above depicts how the curvature of the principal connection is the element of \({\mathfrak{g}}\) corresponding to the vertical component of the negative Lie bracket of the horizontal components of its arguments. The sections used at \({q}\) and \({r}\) are arbitrary, since they don’t affect the vertical component of the loop remainder. If the arguments are pulled back using the identity section, we recover the curvature on the base space \({M}\).
When \({G}\) is a matrix group, we find analogs of equations for curvature on \({M}\) using the relations from the previous section:
\(\displaystyle \begin{aligned}\check{R}_{P} & =\mathrm{d}\check{\Gamma}_{P}+\frac{1}{2}\check{\Gamma}_{P}[\wedge]\check{\Gamma}_{P}\\ \check{R}_{i} & =\mathrm{d}\check{\Gamma}_{i}+\frac{1}{2}\check{\Gamma}_{i}[\wedge]\check{\Gamma}_{i}\\ \mathrm{D}\check{R}_{P} & =0 \end{aligned} \)
Note that \({\check{R}_{P}}\) is a map from 2-forms on \({P}\) to \({\mathfrak{g}}\), where \({G}\) has a left action via the adjoint rep of \({G}\) on \({\mathfrak{g}}\). One can then show that \({\check{R}_{P}}\) is equivariant with respect to this action and that of \({G}\) on 2-forms, i.e. we have
\(\displaystyle g^{*}\check{R}_{P}=g_{\mathrm{Ad}}^{-1}\left(\check{R}_{P}\right). \)
Thus \({\check{R}_{P}}\) is a horizontal equivariant form, and recalling that section we have the expected transformations
\(\displaystyle \begin{aligned}\check{R}_{i} & =\check{g}_{ij}\check{R}_{j}\check{g}_{ij}^{-1},\\ \check{R}_{i}^{\prime} & =\check{\gamma}_{i}\check{R}_{i}\check{\gamma}_{i}^{-1}. \end{aligned} \)
If a flat connection (zero curvature) can be defined on a principal bundle, then the structure group is discrete. If in addition the base space is simply connected, then the bundle is trivial.