Given a fiber bundle \({(E,M,\pi,F)}\) and a continuous map to the base space \({f\colon N\rightarrow M}\), the pullback bundle (AKA induced bundle, pullback of \({E}\) by \({f}\)) is defined as
\(\displaystyle f^{*}(E)\equiv\left\{ \left(n,p\right)\in N\times E\mid f(n)=\pi(p)\right\} , \)
and is a fiber bundle \({(f^{*}(E),N,\pi_{f},F)}\) with the same fiber but base space \({N}\). Projection of \({q=(n,p)\in f^{*}(E)}\) onto \({n}\) is just the bundle projection \({\pi_{f}\colon f^{*}(E)\rightarrow N}\), while projection onto \({p}\) defines a bundle map \({\Phi\colon f^{*}(E)\rightarrow E}\) such that \({\pi\left(\Phi(q)\right)=f\left(\pi_{f}(q)\right)=x\in M}\).
For any topological group \({G}\), there exists a universal principal bundle (AKA universal bundle) \({(EG,BG,G)}\) such that every principal \({G}\)-bundle \({(P,M,G)}\) (with \({M}\) at least a CW-complex) is the pullback of \({EG}\) by some \({f\colon M\rightarrow BG}\). The base space \({BG}\) is called the classifying space for \({G}\). The pullbacks of a principal bundle by two homotopic maps are isomorphic, and thus for a given \({M}\) the homotopy classes of the maps \({f}\) are one-to-one with the isomorphism classes of principal \({G}\)-bundles over \({M}\).
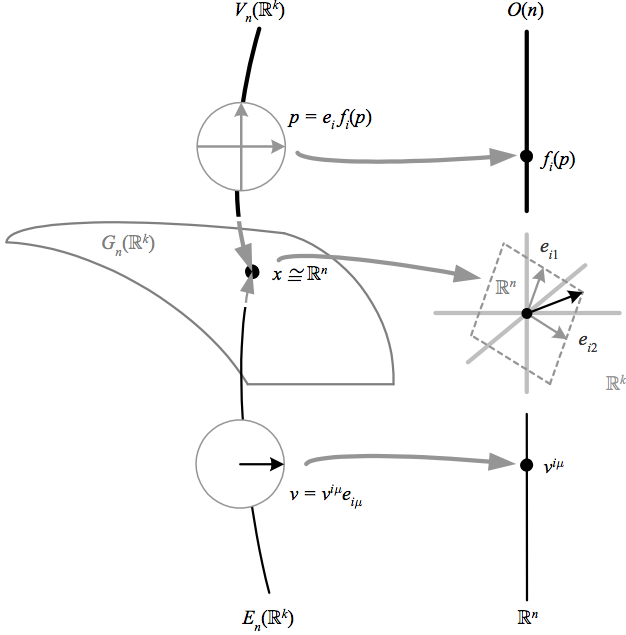
Every vector bundle \({(E,M,\mathbb{K}^{n})}\) is therefore the pullback of the universal vector bundle \({E_{n}(\mathbb{K}^{\infty})}\) (AKA tautological bundle, universal bundle), the vector bundle associated to the universal principal bundle for its structure group. It can be shown that any vector bundle admits an inner product, so we need only consider the structure groups \({O(n)}\) and \({U(n)}\), whose classifying spaces are each a Grassmann manifold (AKA Grassmannian) \({G_{n}(\mathbb{K}^{\infty})}\). This is a limit of the finite-dimensional Grassmann manifold \({G_{n}(\mathbb{K}^{k})}\), which is all \({n}\)-planes in \({\mathbb{K}^{k}}\) through the origin. Each point \({x\in G_{n}(\mathbb{K}^{k})}\) thus corresponds to a copy of \({\mathbb{K}^{n}}\), as does the fiber over \({x}\) in the universal vector bundle, explaining the alternate name “tautological bundle.” The total space of the associated universal principal bundle is the Stiefel manifold \({V_{n}(\mathbb{K}^{\infty})}\), a limit of the finite-dimensional \({V_{n}(\mathbb{K}^{k})}\), defined as all ordered orthonormal \({n}\)-tuples in \({\mathbb{K}^{k}}\); the bundle projection simply sends each \({n}\)-tuple to the \({n}\)-plane containing it.
The above depicts the Grassmann manifold \({G_{n}(\mathbb{R}^{k})}\), which is all \({n}\)-planes in \({\mathbb{R}^{k}}\) through the origin, and which is the base space of the Stiefel manifold \({V_{n}(\mathbb{R}^{k})}\), defined as all ordered orthonormal \({n}\)-tuples in \({\mathbb{R}^{k}}\) where the fiber is \({O(n)}\) and the bundle projection simply sends each \({n}\)-tuple to the \({n}\)-plane containing it. The tautological bundle is the associated vector bundle \({E_{n}(\mathbb{R}^{k})}\) with fiber \({\mathbb{R}^{n}}\), and the universal principal bundle for \({O(n)}\) is the limit \({V_{n}(\mathbb{K}^{\infty})}\).
| Δ Grassmann manifolds can also be denoted \({Gr(n,\mathbb{K}^{k})}\), \({Gr(n,k)}\), \({G_{n,k}}\) or \({g_{n,k}}\) and the order of the parameters are sometimes reversed. Stiefel manifolds have similar alternative notations. |