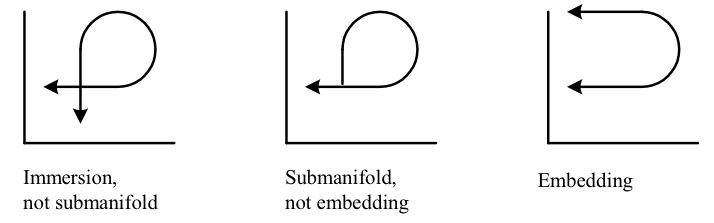
We can generalize and make precise the concept of a surface embedded in 3-dimensional space with the following definitions concerning a differentiable map \({\Phi\colon M^{m}\to N^{n}}\):

• Immersion: \({\mathrm{d}\Phi}\) is injective for all \({p\in M}\); intuitively, a smooth mapping that doesn’t collapse the tangent spaces
• Submanifold: an immersion with \({\Phi}\) injective; intuitively, an immersion that doesn’t intersect itself
• Embedding (AKA imbedding): a submanifold with \({\Phi}\) a homeomorphism onto \({\Phi\left(M\right)}\); intuitively, a submanifold that doesn’t have intersecting limit points

The above depicts \({\mathbb{R}}\) immersed in \({\mathbb{R}^{2}}\); the second immersion approaches a self-intersection in the limit as the line approaches infinity.

The difference in dimension \({\left(n-m\right)}\) is called the codimension of the embedding. The Whitney embedding theorem states that for positive codimension, any \({M^{m}}\) can be immersed in \({\mathbb{R}{}^{(2m-1)}}\) and embedded in \({\mathbb{R}^{2m}}\). Thus we can view differentiable manifolds as generalized surfaces that we study without making reference to the enclosing Euclidean space. The limiting dimension of this theorem is illustrated by noting that the real projective space \({\mathbb{R}\textrm{P}^{m}}\) cannot be embedded in \({\mathbb{R}^{(2m-1)}}\).

A foliation of a manifold \({M^{n}}\), decomposes it into a union of disjoint connected submanifolds \({L_{j}^{k}}\) called leaves, such that there exist coordinates around every point for which the leaves are subspaces with \({n-k}\) coordinates constant. The Frobenius theorem says that a \({k}\)-dimensional subbundle of \({TM}\), a subspace of the tangent space smoothly defined at each point, comprises the tangent bundles of the leaves of a foliation iff the Lie bracket of any two vector fields in the subbundle remains in the subbundle. Two corollaries are that a non-vanishing vector field always defines a flow which is a foliation, and that a frame whose components have vanishing Lie brackets is a coordinate frame for coordinates defined by the orthogonal plane foliations.